
如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC= ,求BN的长.
,求BN的长.

(1)证明见解析;(2)证明见解析;(3)BN=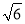 .
.
【解析】
试题分析:(1)根据切线的判定定理得出∠1+∠BCO=90°,即可得出答案;
(2)利用已知得出∠3=∠2,∠4=∠D,再利用相似三角形的判定方法得出即可;
(3)根据已知得出OE的长,进而利用勾股定理得出EC,AC,BC的长,即可得出CD,利用(2)中相似三角形的性质得出NB的长即可.
(1)证明:∵△BCO中,BO=CO,
∴∠B=∠BCO,
在Rt△BCE中,∠2+∠B=90°,
又∵∠1=∠2,
∴∠1+∠BCO=90°,
即∠FCO=90°,
∴CF是⊙O的切线;
(2)证明:如图,∵AB是⊙O直径,
∴∠ACB=∠FCO=90°,
∴∠ACB-∠BCO=∠FCO-∠BCO,
即∠3=∠1,
∴∠3=∠2,
∵∠4=∠D,
∴△ACM∽△DCN;
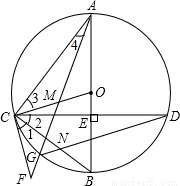
(3)【解析】
∵⊙O的半径为4,即AO=CO=BO=4,
在Rt△COE中,cos∠BOC=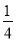 ,
,
∴OE=CO•cos∠BOC=4×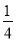 =1,
=1,
由此可得:BE=3,AE=5,由勾股定理可得:
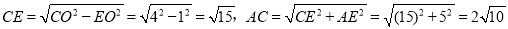 ,
,
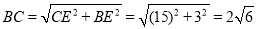 ,
,
∵AB是⊙O直径,AB⊥CD,
∴由垂径定理得:CD=2CE=2 ,
,
∵△ACM∽△DCN,
∴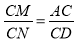 ,
,
∵点M是CO的中点,CM=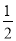 AO=
AO=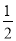 ×4=2,
×4=2,
∴CN=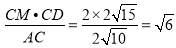 ,
,
∴BN=BC-CN=2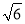 -
-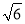 =
=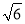 .
.
考点:圆的综合题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源:2013-2014学年山东省初中学业水平考试数学模拟试卷(解析版) 题型:填空题
将正方形图1作如下操作:第1次:分别连接各边中点如图2,得到5个正方形;第2次:将图2左上角正方形按上述方法再分割如图3,得到9个正方形…,以此类推,进行第n次操作得到的正方形的个数是 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省淄博市桓台县九年级中考模拟数学试卷(解析版) 题型:选择题
某市2012年在校初中生的人数约为23万.数230000用科学记数法表示为( )
A.23×104 B.2.3×105 C.0.23×103 D.0.023×106
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市长清区九年级复习调查考试(一模)数学试卷(解析版) 题型:选择题
已知一次函数 ,
, 从
从 中随机取一个值,
中随机取一个值, 从
从 中随机取一个值,则该一次函数的图象经过二、三、四象限的概率为
中随机取一个值,则该一次函数的图象经过二、三、四象限的概率为
A. B.
B.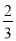 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市九年级中考模拟数学试卷(解析版) 题型:填空题
已知点P(3,-1)关于y轴的对称点Q的坐标是(a+b,1-b),则ab的值为 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:解答题
如图,矩形OABC在平面直角坐标系xoy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O、A两点,直线AC交抛物线于点D。
(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以点A、D、M、N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省泰安市九年级学业模拟考试数学试卷(解析版) 题型:选择题
已知∠I=40°,则∠I的余角度数是
A.150° B.140° C.50° D.60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com