Question

如图，矩形OABC在平面直角坐标系xoy中，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=4,OC=3，若抛物线的顶点在BC边上，且抛物线经过O、A两点，直线AC交抛物线于点D。

（1）求抛物线的解析式；

（2）求点D的坐标；

（3）若点M在抛物线上，点N在x轴上，是否存在以点A、D、M、N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由。

 

 

Answer 1

（1）y=﹣x2+3x；（2）（1，）；（3）N1（2，0），N2（6，0），N3（﹣﹣1，0），N4（﹣1，0）．

【解析】

试题分析：（1）由OA的长度确定出A的坐标，再利用对称性得到顶点坐标，设出抛物线的顶点形式y=a（x-2）2+3，将A的坐标代入求出a的值，即可确定出抛物线解析式；

（2）设直线AC解析式为y=kx+b，将A与C坐标代入求出k与b的值，确定出直线AC解析式，与抛物线解析式联立即可求出D的坐标；

（3）存在，分两种情况考虑：如图所示，当四边形ADMN为平行四边形时，DM∥AN，DM=AN，由对称性得到M（3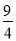， ），即DM=2，故AN=2，根据OA+AN求出ON的长，即可确定出N的坐标；当四边形ADM′N′为平行四边形，可得三角形ADQ全等于三角形N′M′P，M′P=DQ=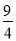，N′P=AQ=3，将y=-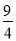代入得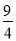：-=-x2+3x，求出x的值，确定出OP的长，由OP+PN′求出ON′的长即可确定出N′坐标．

试题解析：（1）设抛物线顶点为E，根据题意OA=4，OC=3，得：E（2，3），

设抛物线解析式为y=a（x﹣2）2+3，

将A（4，0）坐标代入得：0=4a+3，即a=﹣，

则抛物线解析式为y=﹣（x﹣2）2+3=﹣x2+3x；

（2）设直线AC解析式为y=kx+b（k≠0），

将A（4，0）与C（0，3）代入得：，

解得：，故直线AC解析式为y=﹣x+3，

与抛物线解析式联立得：，解得：或，

则点D坐标为（1，）；

（3）存在，分两种情况考虑：

①当点M在x轴上方时，如答图1所示：

四边形ADMN为平行四边形，DM∥AN，DM=AN，

由对称性得到M（3，），即DM=2，故AN=2，∴N1（2，0），N2（6，0）；

②当点M在x轴下方时，如答图2所示：

过点D作DQ⊥x轴于点Q，过点M作MP⊥x轴于点P，可得△ADQ≌△NMP，

∴MP=DQ=，NP=AQ=3，将yM=﹣代入抛物线解析式得：﹣=﹣x2+3x，

解得：xM=2﹣或xM=2+，∴xN=xM﹣3=﹣﹣1或﹣1，

∴N3（﹣﹣1，0），N4（﹣1，0）．

综上所述，满足条件的点N有四个：N1（2，0），N2（6，0），N3（﹣﹣1，0），N4（﹣1，0）．

考点：二次函数综合题．