
(1)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.

(2)如图,AC是⊙O的直径,弦BD交AC于点E。
①求证:⊿ADE∽⊿BCE;
②如果AD2=AE·AC,求证:CD=CB

1.证明见解析;2.(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1) 通过全等三角形(△AEB≌△DFC)的对应边相等证得BE=CF,由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得BE∥CF.则四边形BECF是平行四边形.
(2) (1)由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠A=∠B,又由对顶角相等,可证得:△ADE∽△BCE;
(2)由AD2=AE•AC,可得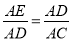 ,又由∠A是公共角,可证得△ADE∽△ACD,又由AC是⊙O的直径,以求得AC⊥BD,由垂径定理即可证得CD=CB.
,又由∠A是公共角,可证得△ADE∽△ACD,又由AC是⊙O的直径,以求得AC⊥BD,由垂径定理即可证得CD=CB.
试题解析:(1) ∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
 ,
,
∴△AEB≌△DFC(ASA),
∴BE=CF.
∵BE⊥AD,CF⊥AD,
∴BE∥CF.
∴四边形BECF是平行四边形.
(2) (1)如图,
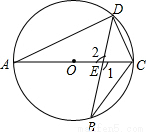
∵∠A与∠B是 对的圆周角,
对的圆周角,
∴∠A=∠B,
又∵∠1=∠2,
∴△ADE∽△BCE;
(2)如图,
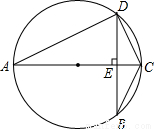
∵AD2=AE•AC,
∴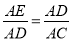 ,
,
又∵∠A=∠A,
∴△ADE∽△ACD,
∴∠AED=∠ADC,
又∵AC是⊙O的直径,
∴∠ADC=90°,
即∠AED=90°,
∴直径AC⊥BD,
∴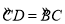 ,
,
∴CD=CB.
考点:1.平行四边形的判定;2.全等三角形的判定与性质;3.圆周角定理;4.相似三角形的判定与性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2013-2014学年山东省淄博市桓台县九年级中考模拟数学试卷(解析版) 题型:选择题
方程2x2+4x-a2=0的根的情况是( )
A.有两个相等的实根 B.无实根 C.有两个不相等的实根 D.只有正根
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市九年级中考模拟数学试卷(解析版) 题型:选择题
假期到了,17名女教师去外地培训,住宿时有2人间和3人间可供租住,每个房间都要住满,她们有几种租住方案( )
A.5种 B.4种 C.3种 D.2种
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:解答题
如图,矩形OABC在平面直角坐标系xoy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O、A两点,直线AC交抛物线于点D。
(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以点A、D、M、N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:选择题
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
(A)2 (B)8 (C)2
(B)8 (C)2 (D)2
(D)2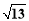

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省泰安市九年级学业模拟考试数学试卷(解析版) 题型:填空题
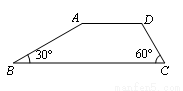
如图,已知梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,AD=4,AB=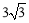 ,则下底BC的长为 __________.
,则下底BC的长为 __________.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省德州市九年级第一次模拟考试数学试卷(解析版) 题型:选择题
若反比例函数 (k<0)的图象上有两点
(k<0)的图象上有两点 (2,
(2,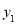 )和
)和 (3,
(3, ),那么
),那么
A. B.
B.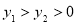
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com