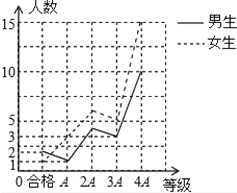
【题目】在初三综合素质评定结束后，为了了解年级的评定情况，现对初三某班的学生进行了评定等级的调查，绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图。

（1）调查发现评定等级为合格的男生有2人，女生有1人，则全班共有_________名学生。

（2）补全女生等级评定的折线统计图。

（3）根据调查情况，该班班主任从评定等级为合格和A的学生中各选1名学生进行交流，请用树形图或表格求出刚好选中一名男生和一名女生的概率。

参考答案：

【答案】（1）50；（2）如下图；（3）

【解析】试题分析：（1）根据合格的男生有2人，女生有1人，得出合格的总人数，再根据评级合格的学生占6%，即可得出全班的人数；

（2）根据折线统计图和扇形统计图以及全班的学生数，即可得出女生评级3A的学生和女生评级4A的学生数，即可补全折线统计图；

（3）根据题意列举出所有可能的情况，再根据概率公式求解即可．

（1）因为合格的男生有2人，女生有1人，共计2+1=3人，

又因为评级合格的学生占6%，

所以全班共有：3÷6%=50（人）；

（2）根据题意得：

女生评级3A的学生是：50×16%-3=8-3=5（人），

女生评级4A的学生是：50×50%-10=25-10=15（人），

（2）根据题意列表得：

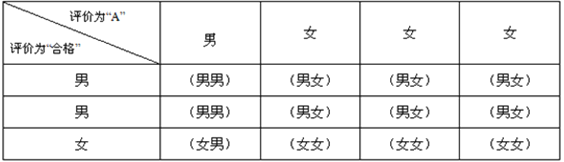
∵共有12种等可能的结果数，其中一名男生和一名女生的共有7种，

∴选中一名男生和一名女生的概率为.

关闭