
ЁОЬтФПЁПРрБШЬиЪтЫФБпаЮЕФбЇЯАЃЌЮвУЧПЩвдЖЈвхЃКгавЛзщЖдНЧЯрЕШЖјСэвЛзщЖдНЧВЛЯрЕШЕФЭЙЫФБпаЮНазіЁАЕШЖдНЧЫФБпаЮЁБЃЎ
ЬНЫїЬхбщ
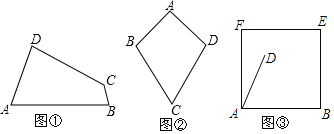
ЃЈ1ЃЉШчЭМЂйЃЌвбжЊЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБЃЌЁЯAЁйЁЯCЃЌЁЯA=70ЁуЃЌЁЯB=80ЁуЃЎЧѓЁЯCЃЌЁЯDЕФЖШЪ§ЃЎ
ЃЈ2ЃЉШчЭМЂкЃЌШєAB=AD=aЃЌCB=CD=bЃЌЧвaЁйbЃЌФЧУДЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБТ№ЃПЪдЫЕУїРэгЩЃЎ
ГЂЪдгІгУ
ЃЈ3ЃЉШчЭМЂлЃЌдкБпГЄЮЊ6ЕФе§ЗНаЮФОАхABEFЩЯВУГіЁАЕШЖдНЧЫФБпаЮЁБABCDЃЌШєвбОШЗЖЈDA=4ЃЌЁЯDAB=60ЁуЃЌЪЧЗёдке§ЗНаЮABEFФкЃЈАќРЈБпЩЯЃЉДцдквЛЕуЕуCЃЌЪЙЫФБпаЮABCDвдЁЯDAB=ЁЯBCDЮЊЕШЖдНЧЕФЫФБпаЮЕФУцЛ§зюДѓЃПШєДцдкЃЌЪдЧѓГіЫФБпаЮABCDЕФзюДѓУцЛ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЁЯC=130ЁуЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉSЫФБпаЮABCD=![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉвбжЊЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБЃЌЁЯAЁйЁЯCЃЌЁЯA=70ЁуЃЌЁЯB=80ЁуЃЌИљОнЖЈвхМДПЩЧѓЕУЁЯDЕФЖШЪ§ЃЌдйгЩЫФБпаЮФкНЧКЭЖЈРэМДПЩЧѓЕУЁЯCЕФЖШЪ§ЃЛЃЈ2ЃЉСЌНгBDЃЌгЩAB=AD=aЃЌCB=CD=bЃЌЧвaЁйbЃЌПЩЕУЁЯABD=ЁЯADCЃЌЁїABDгыЁїCBDВЛЯрЫЦЃЌМДЁЯAЁйЁЯCЃЌдђПЩжЄЕУНсТлЃЛЃЈ3ЃЉСЌНгBDЃЌгЩЕБЁЯDAB=ЁЯBCD=60ЁуЪБЃЌЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБЃЌПЩЕУДЫЪБЕуCдкBDЮЊЯвЕФ![]() ЩЯЃЌМДПЩЕУвЊЪЙЫФБпаЮABCDЕФУцЛ§зюДѓЃЌдђЕуCдкБпBEЩЯЃЌШЛКѓЙ§ЕуDзїDHЁЭABгкЕуHЃЌзїDMЁЭBCгкЕуMЃЌРћгУЙДЙЩЖЈРэЧѓНтМДПЩЧѓЕУД№АИЃЎ
ЩЯЃЌМДПЩЕУвЊЪЙЫФБпаЮABCDЕФУцЛ§зюДѓЃЌдђЕуCдкБпBEЩЯЃЌШЛКѓЙ§ЕуDзїDHЁЭABгкЕуHЃЌзїDMЁЭBCгкЕуMЃЌРћгУЙДЙЩЖЈРэЧѓНтМДПЩЧѓЕУД№АИЃЎ
ЃЈ1ЃЉЁпЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБЃЌЁЯAЁйЁЯCЃЌЁЯA=70ЁуЃЌЁЯB=80ЁуЃЌ
ЁрЁЯD=ЁЯB=80ЁуЃЌ
ЁрЁЯC=360ЁуЉ80ЁуЉ80ЁуЉ70Ёу=130ЁуЃЛ
ЃЈ2ЃЉжЄУїЃКШчЭМ2ЃЌСЌНгBDЃЌ
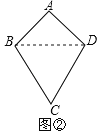
ЁпAB=ADЃЌCB=CDЃЌ
ЁрЁЯABD=ЁЯADBЃЌЁЯCBD=ЁЯCDBЃЌ
ЁрЁЯABD+ЁЯCBD=ЁЯADB+ЁЯCDBЃЌ
ЁрЁЯABC=ЁЯADCЃЌ
ЁпAB=AD=aЃЌCB=CD=bЃЌЧвaЁйbЃЌЧвBD=BDЃЌ
ЁрЁїABDгыЁїCBDВЛЯрЫЦЃЌ
ЁрЁЯAЁйЁЯCЃЌ
ЁрЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌСЌНгBDЃЌ
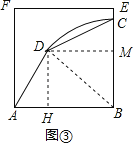
ЕБЁЯDAB=ЁЯBCD=60ЁуЪБЃЌЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБЃЌ
ДЫЪБЕуCдкBDЮЊЯвЕФ![]() ЩЯЃЌ
ЩЯЃЌ
вЊЪЙЫФБпаЮABCDЕФУцЛ§зюДѓЃЌдђЕуCдкБпBEЩЯЃЌ
Й§ЕуDзїDHЁЭABгкЕуHЃЌзїDMЁЭBCгкЕуMЃЌ
дкRtЁїADHжаЃЌЁЯDAH=60ЁуЃЌAD=4ЃЌ
ЁрAH=2ЃЌDH=2![]() ЃЌ
ЃЌ
ЁрBH=ABЉAH=4ЃЌ
ЁпЫФБпаТDHBMЪЧОиаЮЃЌ
ЁрBM=DH=2![]() ЃЌDM=BH=4ЃЌ
ЃЌDM=BH=4ЃЌ
дкRtЁїDMCжаЃЌЁЯDCM=60ЁуЃЌ
ЁрCM=![]() DM=
DM=![]() ЃЌ
ЃЌ
ЁрBC=BM+CM=2![]() +
+![]() =
=![]() ЃЌ
ЃЌ
ЁрSЫФБпаЮABCD=SЁїABD+SЁїBCD=![]() ЁС6ЁС2
ЁС6ЁС2![]() +
+![]() ЁС
ЁС![]() ЁС4=
ЁС4=![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌЯТСаЫЕЗЈВЛе§ШЗЕФЪЧ(ЁЁ ЁЁ)
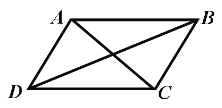
A. ЕБAC=BDЪБЃЌЫФБпаЮABCDЪЧОиаЮ
B. ЕБAB=BCЪБЃЌЫФБпаЮABCDЪЧСтаЮ
C. ЕБACЁЭBDЪБЃЌЫФБпаЮABCDЪЧСтаЮ
D. ЕБЁЯDAB=90ЁуЪБЃЌЫФБпаЮABCDЪЧе§ЗНаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
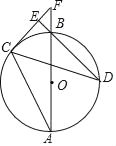
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌCЁЂDЮЊЁбOЩЯВЛЭЌгкAЁЂBЕФСНЕуЃЌЁЯABDЃН2ЁЯBACЃЌСЌНгCDЃЌЙ§ЕуCзїCEЁЭDBЃЌДЙзуЮЊEЃЌжБОЖABгыCEЕФбгГЄЯпЯрНЛгкFЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКCFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЕБBDЃН![]() ЃЌsinFЃН
ЃЌsinFЃН![]() ЪБЃЌЧѓOFЕФГЄЃЎ
ЪБЃЌЧѓOFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
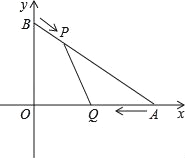
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊЕуAЃЈ4ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌ3ЃЉЃЌЕуPДгЕуBГіЗЂбиBAЗНЯђЯђЕуAдШЫйдЫЖЏЃЌЫйЖШЮЊУПУы1ИіЕЅЮЛГЄЖШЃЌЕуQДгЕуAГіЗЂбиAOЗНЯђЯђЕуOдШЫйдЫЖЏЃЌЫйЖШЮЊУПУы2ИіЕЅЮЛГЄЖШЃЌСЌНгPQЃЎШєЩшдЫЖЏЕФЪБМфЮЊtУыЃЈ0ЃМtЃМ2ЃЉЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЁїAQPЕФУцЛ§ЮЊyЃЌЧѓyгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЯпЖЮPQЧЁКУАбЁїAOBЕФжмГЄКЭУцЛ§ЭЌЪБЦНЗжЃПШєДцдкЃЌЧыЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ4ЃЉСЌНгPOЃЌВЂАбЁїPQOбиQOЗелЃЌЕУЕНЫФБпаЮPQPЁфOЃЌФЧУДЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЫФБпаЮPQPЁфOЮЊСтаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕуQЕФзјБъКЭСтаЮЕФБпГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќФъРДЃЌЁАдкГѕжаЪ§бЇНЬбЇКђзмЪЙгУМЦЫуЦїЪЧЗёжБНггАЯьбЇЩњМЦЫуФмСІЕФЗЂеЙЁБетвЛЮЪЬтЪмЕНСЫЙуЗКЙизЂЃЌЮЊДЫЃЌФГаЃЫцЛњЕїВщСЫnУћбЇЩњЖдДЫЮЪЬтЕФПДЗЈЃЈПДЗЈЗжЮЊШ§жжЃКУЛгагАЯьЃЌгАЯьВЛДѓЃЌгАЯьКмДѓЃЉЃЌВЂНЋЕїВщНсЙћ ЛцжЦГЩШчЯТВЛЭъећЕФЭГМЦБэКЭЩШаЮЭГМЦЭМЃЌИљОнЭГМЦЭМБэЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
nУћбЇЩњЖдЪЙгУМЦЫуЦїгАЯьМЦЫуФмСІЕФЗЂеЙПДЗЈШЫЪ§ЭГМЦБэ
ПДЗЈ | УЛгагАЯь | гАЯьВЛДѓ | гАЯьКмДѓ |
бЇЩњШЫЪ§ЃЈШЫЃЉ | 40 | 60 | m |

ЃЈ1ЃЉЧѓnЕФжЕЃЛ
ЃЈ2ЃЉЭГМЦБэжаЕФm= ЃЛ
ЃЈ3ЃЉЙРМЦИУаЃ1800УћбЇЩњжаШЯЮЊЁАгАЯьКмДѓЁБЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпy1ЃНx2+mx+nЃЌжБЯпy2ЃН2x+1ЃЌХзЮяЯпy1ЕФЖдГЦжсгыжБЯпy2ЕФНЛЕуЮЊЕуAЃЌЧвЕуAЕФзнзјБъЮЊ5ЃЎ
ЃЈ1ЃЉЧѓmЕФжЕЃЛ
ЃЈ2ЃЉШєЕуAгыХзЮяЯпy1ЕФЖЅЕуBЕФОрРыЮЊ4ЃЌЧѓХзЮяЯпy1ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉШєХзЮяЯпy1гыжБЯпy2жЛгавЛИіЙЋЙВЕуЃЌЧѓnЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
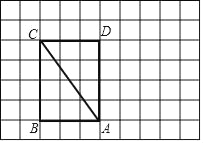
ЁОЬтФПЁПШчЭМЃЌдкУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЕФЭјИёжаЃЌЕуAЃЌBЃЌCЃЌDЖМдкИёЕуЩЯЃЎ
ЃЈЂёЃЉACЕФГЄЮЊЁЁ ЁЁЃЛ
ЃЈЂђЃЉНЋОиаЮABCDШЦЕуAЫГЪБеыа§зЊЕУОиаЮAEFGЃЌЦфжаЃЌЕуCЕФЖдгІЕуFТфдкИёЯпADЕФбгГЄЯпЩЯЃЌЧыгУЮоПЬЖШЕФжБГпдкЭјИёжаЛГіОиаЮAEFGЃЌВЂМђвЊЫЕУїЕуEЃЌGЕФЮЛжУЪЧШчКЮевЕНЕФЃЎЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
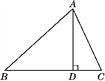
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌADЪЧBCБпЩЯЕФИпЃЌtanBЃНcosЁЯDAC.
ЃЈ1ЃЉЧѓжЄЃКACЃНBDЃЛ
ЃЈ2ЃЉШєsin CЃН![]() ЃЌBCЃН12ЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ЃЌBCЃН12ЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌAB=ACЃЌвдABЮЊжБОЖЕФЁбOгыBCЯрНЛгкЕуDЃЌгыCAЕФбгГЄЯпЯрНЛгкЕуEЃЌЙ§ЕуDзїDFЁЭACгкЕуFЃЎ
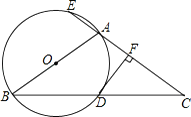
ЃЈ1ЃЉЪдЫЕУїDFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєAC=3AEЃЌЧѓtanCЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com