
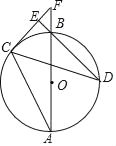
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.
(1)求证:CF是⊙O的切线;
(2)当BD=![]() ,sinF=
,sinF=![]() 时,求OF的长.
时,求OF的长.
【答案】(1)见解析;(2)OF=5.
【解析】
(1)连接OC.先根据等边对等角及三角形外角的性质得出∠3=2∠1,由已知∠4=2∠1,得到∠4=∠3,则OC∥DB,再由CE⊥DB,得到OC⊥CF,根据切线的判定即可证明CF为⊙O的切线;
(2)连接AD.由圆周角定理得出∠D=90°,证出∠BAD=∠F,得出sin∠BAD=sin∠F=![]() ,求出AB=
,求出AB=![]() BD=6,得出OB=OC=3,再由sinF=
BD=6,得出OB=OC=3,再由sinF=![]() 即可求出OF.
即可求出OF.
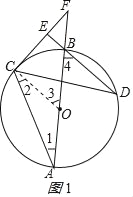
(1)连接OC.如图1所示:
∵OA=OC,
∴∠1=∠2.
又∵∠3=∠1+∠2,
∴∠3=2∠1.
又∵∠4=2∠1,
∴∠4=∠3,
∴OC∥DB.
∵CE⊥DB,
∴OC⊥CF.
又∵OC为⊙O的半径,
∴CF为⊙O的切线;
(2)连接AD.如图2所示:

∵AB是直径,
∴∠D=90°,
∴CF∥AD,
∴∠BAD=∠F,
∴sin∠BAD=sinF=![]() ,
,
∴AB=![]() BD=6,
BD=6,
∴OB=OC=3,
∵OC⊥CF,
∴∠OCF=90°,
∴sinF=![]() ,
,
解得:OF=5.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如表:
周数x | 1 | 2 | 3 | 4 |
价格y(元/千克) | 2 | 2.2 | 2.4 | 2.6 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式;
(2)进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的2.4元/千克,且y与周数x的变化情况满足二次函数y=﹣![]() x2+bx+c,请求出5月份y与x的函数关系式;
x2+bx+c,请求出5月份y与x的函数关系式;
(3)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=![]() x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=﹣
x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=﹣![]() x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上学习了圆周角的概念和性质:“顶点在圆上,两边与圆相交”,“同弧所对的圆周角相等”,小明在课后继续对圆外角和圆内角进行了探究.
下面是他的探究过程,请补充完整:
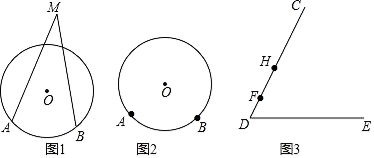
定义概念:顶点在圆外,两边与圆相交的角叫做圆外角,顶点在圆内,两边与圆相交的角叫做圆内角.如图1,∠M为![]() 所对的一个圆外角.
所对的一个圆外角.
(1)请在图2中画出![]() 所对的一个圆内角;
所对的一个圆内角;
提出猜想
(2)通过多次画图、测量,获得了两个猜想:一条弧所对的圆外角______这条弧所对的圆周角;一条弧所对的圆内角______这条弧所对的圆周角;(填“大于”、“等于”或“小于”)
推理证明:
(3)利用图1或图2,在以上两个猜想中任选一个进行证明;
问题解决
经过证明后,上述两个猜想都是正确的,继续探究发现,还可以解决下面的问题.
(4)如图3,F,H是∠CDE的边DC上两点,在边DE上找一点P使得∠FPH最大.请简述如何确定点P的位置.(写出思路即可,不要求写出作法和画图)
查看答案和解析>>
科目:初中数学 来源: 题型:
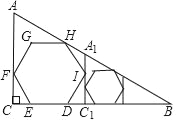
【题目】如图,Rt△ABC中,∠C=Rt∠,AB=2,∠B=30°,正六边形DEFGHI完全落在Rt△ABC内,且DE在BC边上,F在AC边上,H在AB边上,则正六边形DEFGHI的边长为_____,过I作A1C1∥AC,然后在△A1C1B内用同样的方法作第二个正六边形,按照上面的步骤继续下去,则第n个正六边形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两组相同的扑克牌,每组两张,两张牌的牌面数字分别是2和3,从每组牌中各随机摸出一张牌,称为一次试验.
(1)小红与小明用一次试验做游戏,如果摸到的牌面数字相同小红获胜,否则小明获胜,请用列表法或画树状图的方法说明这个游戏是否公平?
(2)小丽认为:“在一次试验中,两张牌的牌面数字和可能为4、5、6三种情况,所以出现‘和为4’的概率是![]() ”,她的这种看法是否正确?说明理由.
”,她的这种看法是否正确?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
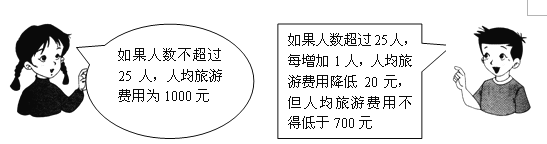 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比特殊四边形的学习,我们可以定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
探索体验
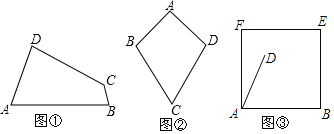
(1)如图①,已知四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°.求∠C,∠D的度数.
(2)如图②,若AB=AD=a,CB=CD=b,且a≠b,那么四边形ABCD是“等对角四边形”吗?试说明理由.
尝试应用
(3)如图③,在边长为6的正方形木板ABEF上裁出“等对角四边形”ABCD,若已经确定DA=4,∠DAB=60°,是否在正方形ABEF内(包括边上)存在一点点C,使四边形ABCD以∠DAB=∠BCD为等对角的四边形的面积最大?若存在,试求出四边形ABCD的最大面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
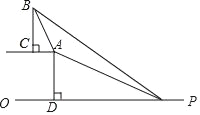
【题目】已知,如图,在坡顶A处的同一水平面上有一座大型纪念碑BC,某同学在斜坡底P处测得该碑的碑顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米到达坡顶A,在坡顶A处又测得该碑的碑顶B的仰角为76°,求纪念碑BC的高度(结果精确到0.1米).(过点A作AD⊥PO,垂足为点D.坡度=AD:PD)(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com