
【题目】今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如表:
周数x | 1 | 2 | 3 | 4 |
价格y(元/千克) | 2 | 2.2 | 2.4 | 2.6 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式;
(2)进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的2.4元/千克,且y与周数x的变化情况满足二次函数y=﹣![]() x2+bx+c,请求出5月份y与x的函数关系式;
x2+bx+c,请求出5月份y与x的函数关系式;
(3)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=![]() x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=﹣
x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=﹣![]() x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
【答案】(1)y=0.2x+1.8;(2)y=![]() x2
x2![]() x+3.1;(3)应在第一周的利润最大,1(元/千克).
x+3.1;(3)应在第一周的利润最大,1(元/千克).
【解析】
(1)从表格看出,x每增加1,y就增加0.2,由此可确定是一次函数关系式,继而代入两点可得出解析式;
(2)把x=1,y=2.8和x=2,y=2.4,分别代入y=﹣![]() x2+bx+c,可求b,c的值,确定二次函数解析式;
x2+bx+c,可求b,c的值,确定二次函数解析式;
(3)根据一次函数,二次函数的性质及自变量的取值范围,求最大利润.
解:(1)通过观察可见四月份周数y与x 的符合一次函数关系式,设这个关系式为:y=kx+b,
则![]() ,
,
解得:![]() ,
,
∴4月份y与x 的函数关系式为y=0.2x+1.8;
(2)将(1,2.8)(2,2.4)代入y=﹣![]() x2+bx+c.
x2+bx+c.
可得: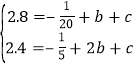
解之: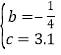
即![]() x2
x2![]()
(3)4月份此种蔬菜利润可表示为:W1=y﹣m=(0.2x+1.8)﹣(![]() x+1.2),即:W1=﹣0.05x+0.6;
x+1.2),即:W1=﹣0.05x+0.6;
由函数解析式可知,四月份的利润随周数的增大而减小,所以应在第一周的利润最大,最大为:W=﹣0.05×1+0.6=0.55(元/千克),
5月份此种蔬菜利润可表示为:W2=y﹣m=(![]() x2
x2![]() x+3.1)﹣(﹣
x+3.1)﹣(﹣![]() x+2),
x+2),
即:W2=![]() x2﹣
x2﹣![]() x+1.1
x+1.1
由函数解析式可知,五月份的利润随周数变化符合二次函数且对称轴为:x=﹣![]() =﹣
=﹣![]() ,
,
即在第1至4周的利润随周数的增大而减小,所以应在第一周的利润最大,最大为:W=![]() ﹣
﹣![]() +1.1=1(元/千克).
+1.1=1(元/千克).


科目:初中数学 来源: 题型:
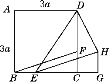
【题目】如图所示,正方形ABCD的边长为3a,两动点E,F分别从顶点B,C同时开始以相同速度沿边BC,CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,B,E,C,G在一条直线上.
(1)若BE=a,求DH的长.
(2)当E点在BC边上的什么位置时,△DHE的面积取得最小值?并求该三角形面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100 m.当气球沿与BA平行地方向飘移10 s后到达C′处时,在A处测得气球的仰角为45°.
(1)求气球的高度(保留根式);
(2)求气球飘移的平均速度(保留根式).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,下列说法不正确的是( )
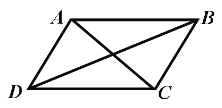
A. 当AC=BD时,四边形ABCD是矩形
B. 当AB=BC时,四边形ABCD是菱形
C. 当AC⊥BD时,四边形ABCD是菱形
D. 当∠DAB=90°时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
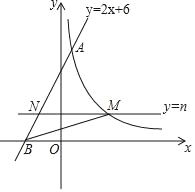
【题目】如图,直线y=2x+6与反比例函数y=![]() (k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的表达式;
(2)观察图象,直接写出当x>0时不等式2x+6﹣![]() <0的解集;
<0的解集;
(3)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)若四边形ABCD为正方形.
①如图①,请直接写出AE与DF的数量关系______________;
②将△EBF绕点B逆时针旋转到图②所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由;
(2)如图③,若四边形ABCD为矩形,BC=mAB,其他条件都不变,将△EBF绕点B逆时针旋转α(0°<α<90°)得到△E′BF′,连接AE′,DF′,请在图③中画出草图,并求出AE′与DF′的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
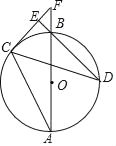
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.
(1)求证:CF是⊙O的切线;
(2)当BD=![]() ,sinF=
,sinF=![]() 时,求OF的长.
时,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
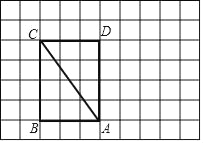
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C,D都在格点上.
(Ⅰ)AC的长为 ;
(Ⅱ)将矩形ABCD绕点A顺时针旋转得矩形AEFG,其中,点C的对应点F落在格线AD的延长线上,请用无刻度的直尺在网格中画出矩形AEFG,并简要说明点E,G的位置是如何找到的. .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com