
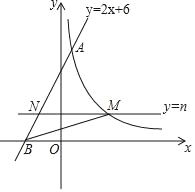
����Ŀ����ͼ��ֱ��y=2x+6�뷴��������y=![]() ��k��0����ͼ���ڵ�A��1��m������x�ύ�ڵ�B��ƽ����x���ֱ��y=n��0��n��6����������������ͼ���ڵ�M����AB�ڵ�N������BM��
��k��0����ͼ���ڵ�A��1��m������x�ύ�ڵ�B��ƽ����x���ֱ��y=n��0��n��6����������������ͼ���ڵ�M����AB�ڵ�N������BM��
��1����m��ֵ�ͷ����������ı���ʽ��
��2���۲�ͼ��ֱ��д����x��0ʱ����ʽ2x+6��![]() ��0�Ľ⼯��
��0�Ľ⼯��
��3��ֱ��y=n��y�᷽��ƽ�ƣ���nΪ��ֵʱ����BMN�����������ֵ�Ƕ��٣�
���𰸡���1�������������Ľ���ʽΪy=![]() ����2��0��x��1����3��
����2��0��x��1����3��![]() ��
��
����������������1���ѵ�A��1��m������ֱ��y=2x+6�����m��ֵ���ٰѵ�A���������y=![]() �����ô���ϵ�������ɽ�����⣻
�����ô���ϵ�������ɽ�����⣻
��2������ͼ��������ĺ���ֵ����ͼ������ĺ���ֵд���𰸼��ɣ�
��3���������κ��������ö��κ��������ʼ��ɽ�����⣻
��⣺��1����ֱ��y=2x+6������A��1��m����
��m=2��1+6=8��
��A��1��8����
�߷���������������A��1��8����
��k=8��
�෴���������Ľ���ʽΪy=![]() ��
��
��2������ʽ2x+6��![]() ��0�Ľ⼯Ϊ0��x��1��
��0�Ľ⼯Ϊ0��x��1��
��3�������⣬��M��N������ΪM��![]() ��n����N��
��n����N��![]() ��n����
��n����
��0��n��6��
��![]() ��0��
��0��
��![]() ��
��![]() ��0
��0
��S��BMN=![]() |MN|��|yM|=
|MN|��|yM|=![]() ����
����![]() ��
��![]() ����n=��
����n=��![]() ��n��3��2+
��n��3��2+![]() ��
��
��n=3ʱ����BMN�����������ֵΪ![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ij��ѧ��¥����һ��������ˮ�ཨ������ŵĵ������Ϊ![]() ������������
������������![]() �ߴ�����һ����У�������õ���������������ˮƽ����Ϊ
�ߴ�����һ����У�������õ���������������ˮƽ����Ϊ![]() ����У�ŵĸ�ԼΪ(��ȷ��
����У�ŵĸ�ԼΪ(��ȷ��![]() ��ˮ�ཨ����ĺ�Ⱥ��Բ���)( )
��ˮ�ཨ����ĺ�Ⱥ��Բ���)( )
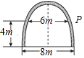
A. 9.2m B. 9.1m C. 9.0m D. 8.9m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
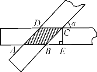
����Ŀ����ͼ��ʾ���������ȶ�Ϊ2cm��ֽ�������ص�����һ�������ǵĽ���Ϊ�����������ص�����(ͼ����Ӱ����)�����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
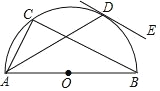
����Ŀ����ͼ����ABC �ڽ��ڰ���O��AB Ϊֱ������ AD ƽ����CAB��DE ����O �ڵ� D��
��1�� ��֤��DE��BC
��2�� �� AD��BC����O �뾶Ϊ 2������CAD �뻡CDΧ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�������1������1�������n���������dz���ɫ�������ͬ��
��1�����������������һ����¼����ɫ��Ȼ��Żأ�ҡ���Ⱥ��ظ���ʵ�飬��������ʵ��������������Ƶ���ȶ���0.5���ң���n��ֵ��
��2���ڣ�1���������£��ȴ������������һ����¼����ɫ���Żأ�ҡ���Ⱥ��ٴӴ�������һ����¼����ɫ�����û���״ͼ�����б��ķ���������Ⱥ�����������ͬ��ɫ��������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ҹ����ʡ���������ظɺ����ܺ��ֵ�Ӱ�죬4�·ݣ�����ij�߲˼۸���������ƣ���ǰ����ÿ�ܵ�ƽ�����ۼ۸�仯�����
����x | 1 | 2 | 3 | 4 |
�۸�y��Ԫ/ǧ�ˣ� | 2 | 2.2 | 2.4 | 2.6 |
��1����۲����еı�������ѧ����һ�κ�������������������κ������й�֪ʶֱ��д��4�·�y��x�ĺ�����ϵʽ��
��2������5�£����ڱ����߲˵����У������߲˵�ƽ�����ۼ۸�y��Ԫ/ǧ�ˣ���5�µ�1�ܵ�2.8Ԫ/ǧ���½�����2�ܵ�2.4Ԫ/ǧ�ˣ���y������x�ı仯���������κ���y����![]() x2+bx+c�������5�·�y��x�ĺ�����ϵʽ��
x2+bx+c�������5�·�y��x�ĺ�����ϵʽ��
��3����4�·ݴ����߲˵Ľ���m��Ԫ/ǧ�ˣ�������x������ĺ�����ϵΪm��![]() x+1.2��5�·ݴ����߲˵Ľ���m��Ԫ/ǧ�ˣ�������x������ĺ�����ϵΪm����
x+1.2��5�·ݴ����߲˵Ľ���m��Ԫ/ǧ�ˣ�������x������ĺ�����ϵΪm����![]() x+2������4�·���5�·ݷֱ�����һ�����۴����߲�һǧ�˵�����������������ֱ��Ƕ��٣�
x+2������4�·���5�·ݷֱ�����һ�����۴����߲�һǧ�˵�����������������ֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
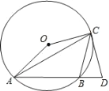
����Ŀ����ͼ,��ABC�ǡ�O�ڽ�������,��ACB=45��,��AOC=150�㣬����C����O���߽�AB�ӳ����ڵ�D��
(1)��֤��CD=CB��(2)�����O�İ뾶Ϊ![]() ����AC�ij���
����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
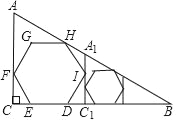
����Ŀ����ͼ��Rt��ABC�У���C��Rt�ϣ�AB��2����B��30������������DEFGHI��ȫ����Rt��ABC�ڣ���DE��BC���ϣ�F��AC���ϣ�H��AB���ϣ�����������DEFGHI�ı߳�Ϊ_____����I��A1C1��AC��Ȼ������A1C1B����ͬ���ķ������ڶ����������Σ���������IJ��������ȥ�����n���������εı߳�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
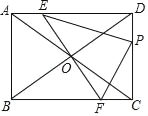
����Ŀ����ͼ���ھ���ABCD�У�AB��3��BC��4�����Խ���AC�ƶԽ��߽���O��ת���ֱ�AD��BC�ڵ�E��F����P�DZ�DC�ϵ�һ�����㣬�ұ���DP��AE������PE��PF����AE��x��0��x��3����
��1����գ�PC���� ����FC���� �������ú�x�Ĵ���ʽ��ʾ��
��2�����PEF�������Сֵ��
��3�����˶������У�PE��PF�Ƿ�����������������x��ֵ��������������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com