
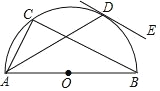
【题目】如图,△ABC 内接于半⊙O,AB 为直径,弦 AD 平分∠CAB,DE 切⊙O 于点 D.
(1) 求证:DE∥BC
(2) 若 AD=BC,⊙O 半径为 2,求∠CAD 与弧CD围成区域的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接OD.只要证明DE⊥OD,BC⊥OD即可解决问题;
(2)只要证明△COD是等边三角形,可得∠CDO=∠DOB=60°,推出CD∥AB,推出S△ACD=S△COD,可得∠CAD与![]() 围成区域的面积=扇形OCD的面积,由此即可解决问题.
围成区域的面积=扇形OCD的面积,由此即可解决问题.
(1)证明:连接OD.
∵DE是⊙O切线,
∴OD⊥DE,
∵AD平分∠CAB,
∴∠DAC=∠DAB,
∴![]() =
=![]() ,
,
∴OD⊥BC,
∴DE∥BC.
(2)∵AD=BC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,∵
,∵![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴∠COD=∠BOD=60°,
∵OC=OD,
∴△COD是等边三角形,
∴∠CDO=∠DOB=60°,
∴CD∥AB,
∴S△ACD=S△COD,
∴∠CAD与![]() 围成区域的面积=扇形OCD的面积=
围成区域的面积=扇形OCD的面积=![]() =
=![]() π.
π.


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与直线
与直线![]() 交于点A,点A的横坐标为
交于点A,点A的横坐标为![]() ,且直线
,且直线![]() 与x轴交于点B,与y轴交于点D,直线
与x轴交于点B,与y轴交于点D,直线![]() 与y轴交于点C.
与y轴交于点C.
(1)求点A的坐标及直线![]() 的函数表达式;
的函数表达式;
(2)连接![]() ,求
,求![]() 的面积.
的面积.
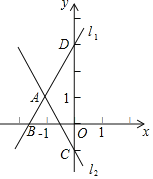
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线![]() 上,转轴
上,转轴![]() 到地面的距离
到地面的距离![]() ,小亮在荡秋千过程中,当秋千摆动到最高点
,小亮在荡秋千过程中,当秋千摆动到最高点![]() 时,测得点
时,测得点![]() 到
到![]() 的距离
的距离![]() ,点
,点![]() 到地面的距离
到地面的距离![]() :当他从
:当他从![]() 处摆动到
处摆动到![]() 处时,有
处时,有![]() .
.
(1)求![]() 到
到![]() 的距离;
的距离;
(2)求![]() 到地面的距离.
到地面的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°,BD、CE分别是△ABC、△BCD的角平分线.则图中的等腰三角形有( )

A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,公路上有![]() 三个车站,一辆汽车从
三个车站,一辆汽车从![]() 站以速度
站以速度![]() 匀速驶向
匀速驶向![]() 站,到达
站,到达![]() 站后不停留,以速度
站后不停留,以速度![]() 匀速驶向
匀速驶向![]() 站,汽车行驶路程
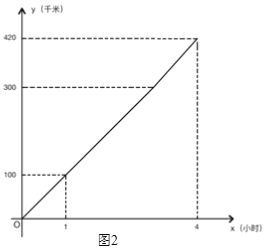
站,汽车行驶路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数图象如图2所示.
(小时)之间的函数图象如图2所示.
(1)求![]() 与
与![]() 之间的函数关系式及自变量的取值范围.
之间的函数关系式及自变量的取值范围.
(2)汽车距离C站20千米时已行驶了多少时间?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,以AB为直径作⊙O恰好与CD相切.
(1)求证:AD+BC=CD;
(2)若E为OA的中点,连结CE并延长交DA的延长线于F,当AE=AF时,求sin∠DCF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料:我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、十字相乘法等等,其中十字相乘法在高中应用较多.
十字相乘法:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图),如:将式子![]() 和
和![]() 分解因式,如图:
分解因式,如图:
![]() ;
;
![]() .
.
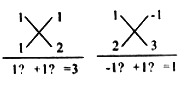
请你仿照以上方法,探索解决下列问题:
(1)分解因式:![]() ;
;
(2)分解因式:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的转盘,分成三个相同的扇形,指针位置固定转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,当作指向右边的扇形).
(1)求事件“转动一次,得到的数恰好是0”发生的概率;
(2)写出此情景下一个不可能发生的事件.
(3)用树状图或列表法,求事件“转动两次,第一次得到的数与第二次得到的数绝对值相等”发生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ADB≌△EDB,△BDE≌△CDE,B,E,C在一条直线上.下列结论:①BD是∠ABE的平分线;②AB⊥AC;③∠C=30°;④线段DE是△BDC的中线;⑤AD+BD=AC.其中正确的有( )个.
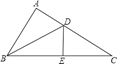
A.2B.3C.4D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com