
【题目】如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,以AB为直径作⊙O恰好与CD相切.
(1)求证:AD+BC=CD;
(2)若E为OA的中点,连结CE并延长交DA的延长线于F,当AE=AF时,求sin∠DCF.

【答案】(1)详见解析;(2)sin∠DCF=![]() .
.
【解析】
(1)作OH⊥CD于H,如图,根据切线的性质得到点H为切点,再证明AD和BC都与⊙O相切,则根据切线长定理得到DA=DH,CB=CH,于是有AD+BC=DH+CH=CD;
(2)先判断△AEF为等腰直角三角形得到∠F=45°,再判断△OBC为等腰直角三角形得BE=BC,作DG⊥BC于G,如图,易得四边形ABGD为矩形,则设AE=AF=x,AD=y,所以BE=BC=3x,CD=y+3x,DG=4x,CG=CB-BG=3x-y,接着在Rt△DGC中利用勾股定理可计算出y=![]() x,则CD=
x,则CD=![]() x,DF=
x,DF=![]() x;作DK⊥CF于K,如图,则△KDF为等腰直角三角形,于是DK=
x;作DK⊥CF于K,如图,则△KDF为等腰直角三角形,于是DK=![]() DF=
DF=![]() x,然后在Rt△CDK中根据正弦的定义求解.
x,然后在Rt△CDK中根据正弦的定义求解.
(1)证明:作OH⊥CD于H,如图,
∵以AB为直径作⊙O与CD相切,
∴点H为切点,
∵∠ABC=90°,AD∥BC,
∴AD⊥AB,BC⊥AB,
∴AD和BC都与⊙O相切,
∴DA=DH,CB=CH,
∴AD+BC=DH+CH=CD;
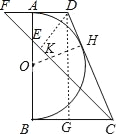
(2)解:∵AE=AF,∠EAF=90°,
∴△AEF为等腰直角三角形,
∴∠F=45°,
∵AF∥BC,
∴∠FCB=45°,
∴△OBC为等腰直角三角形,
∴BE=BC,
作DG⊥BC于G,如图,易得四边形ABGD为矩形,
设AE=AF=x,AD=y,则BE=BC=3x,
∴CD=y+3x,DG=4x,CG=CB﹣BG=3x﹣y,
在Rt△DGC中,∵DG2+CG2=CD2,
∴(4x)2+(3x﹣y)2=(y+3x)2,
∴y=![]() x,
x,
∴CD=![]() x+3x=
x+3x=![]() x,DF=x+
x,DF=x+![]() x=
x=![]() x,
x,
作DK⊥CF于K,如图,则△KDF为等腰直角三角形,
∴DK=![]() DF=
DF=![]() x,
x,
在Rt△CDK中,sin∠DCK=![]() =
=![]() =
=![]() ,
,
即sin∠DCF=![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①c<0;②2a+b=0;③a+b+c<0;④b2-4ac<0,其中正确的有( )
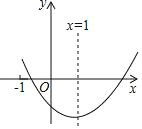
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
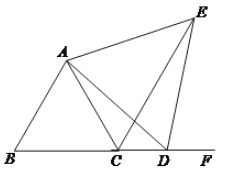
【题目】如图, △ABC是等边三角形,D是BC延长线上任意一点,以AD为一边向右侧作等边△ADE,连接CE.
1.求证:△CAE≌△BAD;
2.判断直线AB与EC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
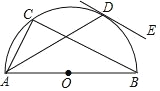
【题目】如图,△ABC 内接于半⊙O,AB 为直径,弦 AD 平分∠CAB,DE 切⊙O 于点 D.
(1) 求证:DE∥BC
(2) 若 AD=BC,⊙O 半径为 2,求∠CAD 与弧CD围成区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间小明和小丽相约到苏州乐园游玩,小丽乘私家车从上海出发30分钟后,小明乘坐火车从上海出发,先到苏州北站,然后再乘出租车去游乐园(换乘时间忽略不计),两人恰好同时到达苏州乐园,他们离上海的距离y(千米)与乘车时间t(小时)的关系如图所示,请结合图象信息解决下面问题:
(1)本次火车的平均速度_________千米/小时?
(2)当小明到达苏州北站时,小丽离苏州乐园的距离还有多少千米?
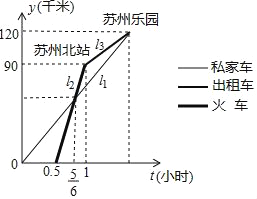
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕.若AB=9,BC=3,试求以折痕EF为边长的正方形面积( )
A. 11 B. 10 C. 9 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为( )
),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com