
【题目】如图, △ABC是等边三角形,D是BC延长线上任意一点,以AD为一边向右侧作等边△ADE,连接CE.
1.求证:△CAE≌△BAD;
2.判断直线AB与EC的位置关系,并说明理由.
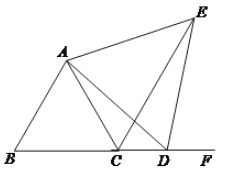
【答案】(1)见解析;(2)EC∥AB,理由见解析.
【解析】
(1)根据△ADE与△ABC都是等边三角形,得到AC=AB,AE=AD,∠DAE=∠BAC=60°,从而得到∠DAE+∠CAD=∠BAC+∠CAD、即∠CAE=∠BAD,利用SAS证得△CAE≌△BAD;
(2)由△CAE≌△BAD,得到∠ACE=∠B=60°,∠ACE=∠BAC=60°,利用内错角相等证得EC∥AB.
(1)∵△ADE与△ABC都是等边三角形,
∴ AC = AB,AE = AD,∠DAE =∠BAC =60°.
∴ ∠DAE+∠CAD =∠BAC+∠CAD. 即∠CAE =∠BAD.
∴在△CAE与△BAD中,
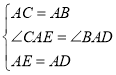
∴ △CAE≌△BAD.
(2)EC∥AB.
由△CAE≌△BAD,
∴∠ACE=∠B=60°,
∴∠ACE=∠BAC=60°,
∴EC∥AB.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】过正方形![]() (四边都相等,四个角都是直角)的顶点
(四边都相等,四个角都是直角)的顶点![]() 作一条直线
作一条直线![]() .
.
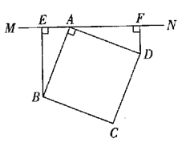
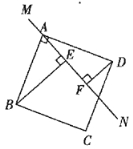
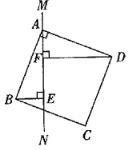
图(1) 图(2) 图(3)
(1)当![]() 不与正方形任何一边相交时,过点
不与正方形任何一边相交时,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() 如图(1),请写出
如图(1),请写出![]() ,
,![]() ,
,![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
(2)若改变直线![]() 的位置,使
的位置,使![]() 与
与![]() 边相交如图(2),其它条件不变,
边相交如图(2),其它条件不变,![]() ,
,![]() ,
,![]() 的关系会发生变化,请直接写出
的关系会发生变化,请直接写出![]() ,
,![]() ,
,![]() 的数量关系,不必证明;
的数量关系,不必证明;
(3)若继续改变直线![]() 的位置,使
的位置,使![]() 与
与![]() 边相交如图(3),其它条件不变,
边相交如图(3),其它条件不变,![]() ,
,![]() ,
,![]() 的关系又会发生变化,请直接写出
的关系又会发生变化,请直接写出![]() ,
,![]() ,
,![]() 的数量关系,不必证明.
的数量关系,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
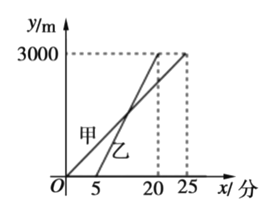
【题目】赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点![]() 驶向终点
驶向终点![]() ,在整个行程中,龙舟离开起点的距离
,在整个行程中,龙舟离开起点的距离![]() (米)与时间
(米)与时间![]() (分钟)的对应关系如图所示,请结合图象解答下列问题:
(分钟)的对应关系如图所示,请结合图象解答下列问题:
(1)起点![]() 与终点
与终点![]() 之间相距
之间相距 ![]() .
.
(2)分别求甲、乙两支龙舟队的![]() 与
与![]() 函数关系式;
函数关系式;
(3)甲龙舟队出发多少时间时两支龙舟队相距200米?
查看答案和解析>>
科目:初中数学 来源: 题型:
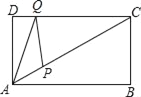
【题目】如图,矩形ABCD中,AD=5,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°,BD、CE分别是△ABC、△BCD的角平分线.则图中的等腰三角形有( )

A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过点C的切线,垂足为点D,AB的延长线交切线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB =4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,以AB为直径作⊙O恰好与CD相切.
(1)求证:AD+BC=CD;
(2)若E为OA的中点,连结CE并延长交DA的延长线于F,当AE=AF时,求sin∠DCF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里有4排日光灯,每排灯各由一个开关控制,但灯的排数序号与开关序号不一定对应,其中控制第二排灯的开关已坏(闭合开关时灯也不亮).
(1)将4个开关都闭合时,教室里所有灯都亮起的概率是 ;
(2)在4个开关都闭合的情况下,不知情的雷老师准备做光学实验,由于灯光太强,他需要关掉部分灯,于是随机将4个开关中的2个断开,请用列表或画树状图的方法,求恰好关掉第一排与第三排灯的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建立模型:
如图1,等腰Rt△ABC中,∠ABC=90°,CB=BA,直线ED经过点B,过A作AD⊥ED于D,过C作CE⊥ED于E.则易证△ADB≌△BEC.这个模型我们称之为“一线三垂直”.它可以把倾斜的线段AB和直角∠ABC转化为横平竖直的线段和直角,所以在平面直角坐标系中被大量使用.
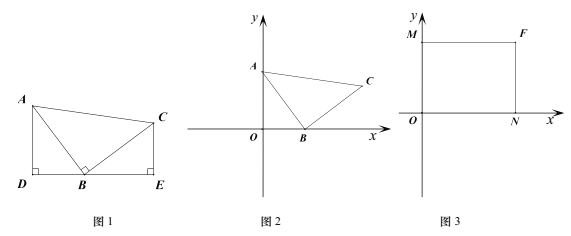
模型应用:
(1)如图2,点A(0,4),点B(3,0),△ABC是等腰直角三角形.
①若∠ABC=90°,且点C在第一象限,求点C的坐标;
②若AB为直角边,求点C的坐标;
(2)如图3,长方形MFNO,O为坐标原点,F的坐标为(8,6),M、N分别在坐标轴上,P是线段NF上动点,设PN=n,已知点G在第一象限,且是直线y=2x一6上的一点,若△MPG是以G为直角顶点的等腰直角三角形,请直接写出点G的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com