
ЁОЬтФПЁПНЈСЂФЃаЭЃК
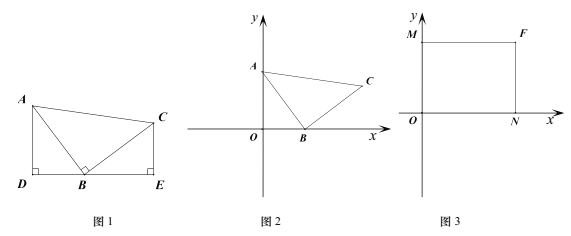
ШчЭМ1ЃЌЕШбќRtЁїABCжаЃЌЁЯABCЃН90ЁуЃЌCBЃНBAЃЌжБЯпEDОЙ§ЕуBЃЌЙ§AзїADЁЭEDгкDЃЌЙ§CзїCEЁЭEDгкE.дђвзжЄЁїADBЁеЁїBEC.етИіФЃаЭЮвУЧГЦжЎЮЊЁАвЛЯпШ§ДЙжБЁБ.ЫќПЩвдАбЧуаБЕФЯпЖЮABКЭжБНЧЁЯABCзЊЛЏЮЊКсЦНЪњжБЕФЯпЖЮКЭжБНЧЃЌЫљвддкЦНУцжБНЧзјБъЯЕжаБЛДѓСПЪЙгУ.
ФЃаЭгІгУЃК
(1)ШчЭМ2ЃЌЕуAЃЈ0ЃЌ4)ЃЌЕуB(3ЃЌ0ЃЉЃЌЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЎ
ЂйШєЁЯABCЃН90ЁуЃЌЧвЕуCдкЕквЛЯѓЯоЃЌЧѓЕуCЕФзјБъЃЛ
ЂкШєABЮЊжБНЧБпЃЌЧѓЕуCЕФзјБъЃЛ
(2)ШчЭМ3ЃЌГЄЗНаЮMFNOЃЌOЮЊзјБъдЕуЃЌFЕФзјБъЮЊЃЈ8ЃЌ6ЃЉЃЌMЁЂNЗжБ№дкзјБъжсЩЯЃЌPЪЧЯпЖЮNFЩЯЖЏЕуЃЌЩшPNЃНnЃЌвбжЊЕуGдкЕквЛЯѓЯоЃЌЧвЪЧжБЯпyЃН2xвЛ6ЩЯЕФвЛЕуЃЌШєЁїMPGЪЧвдGЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЕуGЕФзјБъ.
ЁОД№АИЁПЃЈ1ЃЉЂйЃЈ7,3ЃЉЃЛЂкЃЈ7,3ЃЉЁЂЃЈ4,7ЃЉЁЂЃЈ-4,1ЃЉЁЂЃЈ-1,-3ЃЉЃЛЃЈ2ЃЉЃЈ4ЃЌ2ЃЉЁЂ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉЂйЙ§CзїCDДЙжБгкxжсЙЙдьЁАвЛЯпШ§ДЙжБЁБЃЌдйИљОнШЋЕШШ§НЧаЮЕФаджЪЧѓНтМДПЩЃЛЂкЕуCгаЫФДІЃЌЗжБ№зїГіЭМаЮЃЌИљОнЁАвЛЯпШ§ДЙжБЁБЛђЖдГЦЧѓНтМДПЩЃЛЃЈ2ЃЉЕБЕуGЮЊжБНЧЖЅЕуЪБЃЌЗжЕуGдкОиаЮMFNOЕФФкВПгыЭтВПСНжжЧщПіЙЙдьЁАвЛЯпШ§ДЙжБЁБЧѓНтМДПЩЃЎ
ЃЈ1ЃЉЂйШчЭМЃЌЙ§CзїCDДЙжБгкxжсЃЌ

ИљОнЁАвЛЯпШ§ДЙжБЁБПЩЕУЁїAOBЁеЁїBDCЃЌЁрAO=BDЃЌOB=CDЃЌ
ЁпЕуAЃЈ0ЃЌ4)ЃЌЕуB(3ЃЌ0ЃЉЃЌЁрAO=4ЃЌOB=3 ЃЌ
ЁрOD=3+4=7ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ7,3ЃЉЃЛ
ЂкШчЭМЃЌШєABЮЊжБНЧБпЃЌЕуCЕФЮЛжУПЩга4ДІЃЌ
aЁЂШєЕуCдкЂйЕФЮЛжУДІЃЌдђЕуCЕФзјБъЮЊЃЈ7,3ЃЉЃЛ
bЁЂШєЕуCдк![]() ЕФЮЛжУДІЃЌЭЌРэПЩЕУЃЌдђЕу
ЕФЮЛжУДІЃЌЭЌРэПЩЕУЃЌдђЕу![]() ЕФзјБъЮЊЃЈ4,7ЃЉЃЛ
ЕФзјБъЮЊЃЈ4,7ЃЉЃЛ
cЁЂШєЕуCдк![]() ЕФЮЛжУДІЃЌдђ
ЕФЮЛжУДІЃЌдђ![]() ЁЂ
ЁЂ![]() ЙигкЕуAЖдГЦЃЌ
ЙигкЕуAЖдГЦЃЌ
ЁпЕуAЃЈ0ЃЌ4)ЃЌЕу![]() ЃЈ4,7ЃЉЃЌЁрЕу
ЃЈ4,7ЃЉЃЌЁрЕу![]() ЕФзјБъЮЊЃЈ-4,1ЃЉЃЛ
ЕФзјБъЮЊЃЈ-4,1ЃЉЃЛ
dЁЂШєЕуCдк![]() ЕФЮЛжУДІЃЌдђ
ЕФЮЛжУДІЃЌдђ![]() ЁЂCЙигкЕуBЖдГЦЃЌ
ЁЂCЙигкЕуBЖдГЦЃЌ
ЁпЕуB(3ЃЌ0ЃЉЃЌЕуCЃЈ7,3ЃЉЃЌЁрЕу![]() ЕФзјБъЮЊЃЈ-1,-3ЃЉЃЛ
ЕФзјБъЮЊЃЈ-1,-3ЃЉЃЛ
злЩЯЃЌЕуCЕФзјБъЮЊЃЈ7,3ЃЉЁЂЃЈ4,7ЃЉЁЂЃЈ-4,1ЃЉЁЂЃЈ-1,-3ЃЉЃЛ
ЃЈ2ЃЉЕБЕуGЮЛгкжБЯпy=2x-6ЩЯЪБЃЌЗжСНжжЧщПіЃК
ЂйЕБЕуGдкОиаЮMFNOЕФФкВПЪБЃЌШчЭМЃЌЙ§GзїxжсЕФЦНааЯпABЃЌНЛyжсгкAЃЌНЛжБЯпNFгкЕуBЃЌЩшGЃЈxЃЌ2x-6ЃЉЃЛ
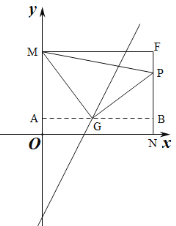
дђOA=2x-6ЃЌAM=6-ЃЈ2x-6ЃЉ=12-2xЃЌBG=AB-AG=8-xЃЛ
дђЁїMAGЁеЁїGBPЃЌЕУAM =BGЃЌ
МДЃК12-2x=8-xЃЌНтЕУx=4ЃЌ
ЁрGЃЈ4ЃЌ2ЃЉЃЛ
ЕБЕуGдкОиаЮMFNOЕФЭтВПЪБЃЌШчЭМЃЌЙ§GзїxжсЕФЦНааЯпABЃЌНЛyжсгкAЃЌНЛжБЯпNFЕФбгГЄЯпгкЕуBЃЌЩшGЃЈxЃЌ2x-6ЃЉЃЛ
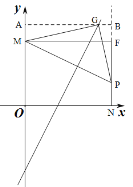
дђOA=2x-6ЃЌAM=ЃЈ2x-6ЃЉ-6=2x-12ЃЌBG=AB-AG=8-xЃЛ
дђЁїMAGЁеЁїGBPЃЌЕУAM =BGЃЌ
МДЃК2x-12=8-xЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрG ![]() ЃЛ
ЃЛ
злЩЯЃЌGЕуЕФзјБъЮЊЃЈ4ЃЌ2ЃЉЁЂ![]() .
.


 ГхДЬ100Зж1КХОэЯЕСаД№АИ
ГхДЬ100Зж1КХОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
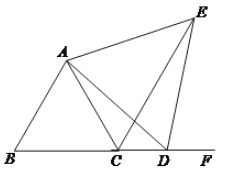
ЁОЬтФПЁПШчЭМ, ЁїABCЪЧЕШБпШ§НЧаЮЃЌDЪЧBCбгГЄЯпЩЯШЮвтвЛЕуЃЌвдADЮЊвЛБпЯђгвВрзїЕШБпЁїADEЃЌСЌНгCE.
1.ЧѓжЄЃКЁїCAEЁеЁїBADЃЛ
2.ХаЖЯжБЯпABгыECЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбГЄЗНаЮжНЦЌABCDелЕўЃЌЪЙЖЅЕуAгыЖЅЕуCжиКЯдквЛЦ№ЃЌEFЮЊелКлЃЎШєAB=9ЃЌBC=3ЃЌЪдЧѓвделКлEFЮЊБпГЄЕФе§ЗНаЮУцЛ§ЃЈЁЁЁЁЃЉ
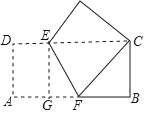
A. 11 B. 10 C. 9 D. 16
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=Љ![]() x2+mx+nгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпЕФЖдГЦжсНЛxжсгкЕуDЃЌвбжЊAЃЈЉ1ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉЃЎ
x2+mx+nгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпЕФЖдГЦжсНЛxжсгкЕуDЃЌвбжЊAЃЈЉ1ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїPCDЪЧвдCDЮЊбќЕФЕШбќШ§НЧаЮЃПШчЙћДцдкЃЌжБНгаДГіPЕуЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕуEЪБЯпЖЮBCЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуEзїxжсЕФДЙЯпгыХзЮяЯпЯрНЛгкЕуFЃЌЕБЕуEдЫЖЏЕНЪВУДЮЛжУЪБЃЌЫФБпаЮCDBFЕФУцЛ§зюДѓЃПЧѓГіЫФБпаЮCDBFЕФзюДѓУцЛ§МАДЫЪБEЕуЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯп![]() ОЙ§ЕуЃЈ2ЃЌ3ЃЉЃЌЖдГЦжсЮЊжБЯпx =1.
ОЙ§ЕуЃЈ2ЃЌ3ЃЉЃЌЖдГЦжсЮЊжБЯпx =1.
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЙћДЙжБгкyжсЕФжБЯпlгыХзЮяЯпНЛгкСНЕуAЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌBЃЈ
ЃЉЃЌBЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌЦфжа
ЃЉЃЌЦфжа![]() ЃЌ
ЃЌ ![]() ЃЌгыyжсНЛгкЕуCЃЌЧѓBC
ЃЌгыyжсНЛгкЕуCЃЌЧѓBC![]() ACЕФжЕЃЛ
ACЕФжЕЃЛ
ЃЈ3ЃЉНЋХзЮяЯпЯђЩЯЛђЯђЯТЦНвЦЃЌЪЙаТХзЮяЯпЕФЖЅЕуТфдкxжсЩЯЃЌдХзЮяЯпЩЯвЛЕуPЦНвЦКѓЖдгІЕуЮЊЕуQЃЌШчЙћOP=OQЃЌжБНгаДГіЕуQЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
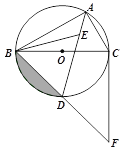
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌBCЮЊЁбOЕФжБОЖЃЌЕуEЮЊЁїABCЕФФкаФЃЌСЌНгAEВЂбгГЄНЛЁбOгкDЕуЃЌСЌНгBDВЂбгГЄжСFЃЌЪЙЕУBD![]() DFЃЌСЌНгCFЁЂBEЃЎ
DFЃЌСЌНгCFЁЂBEЃЎ
ЃЈ1ЃЉЧѓжЄЃКDB![]() DEЃЛ
DEЃЛ
ЃЈ2ЃЉЧѓжЄЃКжБЯпCFЮЊЁбOЕФЧаЯпЃЛ
ЃЈ3ЃЉШєCF![]() 4ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§.
4ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌRtЁїOABЕФЖЅЕуAдкxжсЕФе§АыжсЩЯЃЎЖЅЕуBЕФзјБъЮЊЃЈ3ЃЌ![]() ЃЉЃЌЕуCЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌЧвЁЯAOB=30ЁуЕуPЮЊаББпOBЩЯЕФвЛИіЖЏЕуЃЌдђPA+PCЕФзюаЁжЕЮЊЃЈЁЁ ЁЁЃЉ
ЃЉЃЌЕуCЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌЧвЁЯAOB=30ЁуЕуPЮЊаББпOBЩЯЕФвЛИіЖЏЕуЃЌдђPA+PCЕФзюаЁжЕЮЊЃЈЁЁ ЁЁЃЉ

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуEЪЧе§ЗНаЮABCDЭтвЛЕуЃЌСЌНгAEЁЂBEКЭDEЃЌЙ§ЕуAзїAEЕФДЙЯпНЛDEгкЕуPЃЎШєAEЃНAPЃН1ЃЌPBЃН3ЃЎЯТСаНсТлЃКЂйЁїAPDЁеЁїAEBЃЛЂкEBЁЭEDЃЛЂлЕуBЕНжБЯпAEЕФОрРыЮЊ![]() ЃЛЂмSе§ЗНаЮABCDЃН8+
ЃЛЂмSе§ЗНаЮABCDЃН8+![]() ЃЎдђе§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
ЃЎдђе§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
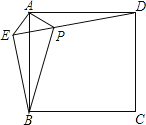
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯп![]() ОЙ§ЕуAЃЈ
ОЙ§ЕуAЃЈ![]() ЃЌ0ЃЉЃЌBЃЈ
ЃЌ0ЃЉЃЌBЃЈ![]() ЃЌ0ЃЉЃЌЧвгыyжсЯрНЛгкЕуCЃЎ
ЃЌ0ЃЉЃЌЧвгыyжсЯрНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓетЬѕХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЧѓЁЯACBЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЩшЕуDЪЧЫљЧѓХзЮяЯпЕквЛЯѓЯоЩЯвЛЕуЃЌЧвдкЖдГЦжсЕФгвВрЃЌЕуEдкЯпЖЮACЩЯЃЌЧвDEЁЭACЃЌЕБЁїDCEгыЁїAOCЯрЫЦЪБЃЌЧѓЕуDЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com