
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点(2,3),对称轴为直线x =1.
经过点(2,3),对称轴为直线x =1.
(1)求抛物线的表达式;
(2)如果垂直于y轴的直线l与抛物线交于两点A(![]() ,
, ![]() ),B(
),B(![]() ,
, ![]() ),其中
),其中![]() ,
, ![]() ,与y轴交于点C,求BC
,与y轴交于点C,求BC![]() AC的值;
AC的值;
(3)将抛物线向上或向下平移,使新抛物线的顶点落在x轴上,原抛物线上一点P平移后对应点为点Q,如果OP=OQ,直接写出点Q的坐标.
【答案】(1)![]() ;(2)BC-AC=2;(3)点Q的坐标为(
;(2)BC-AC=2;(3)点Q的坐标为(![]() )或(
)或(![]() ).
).
【解析】试题分析:(1)由抛物线![]() 经过点(2,3),对称轴为直线x =1,利用待定系数法即可得;
经过点(2,3),对称轴为直线x =1,利用待定系数法即可得;
(2)如图,设l与对称轴交于点M,根据抛物线的对称性,可知AM=BM, AM=AC+CM,BC=BM+CM,推导即可得;
(3)由OP=OQ可知P、Q两点关于x轴对称,求出平移后的解析式,表示出P、Q的坐标,根据关于x轴对称的点的性质即可求得 .
试题解析:(1)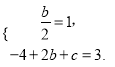 ,解得
,解得![]() ,
,
∴![]() ;
;
(2)如图,设l与对称轴交于点M,则有CM=1,
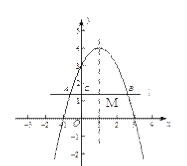
由抛物线的对称性可得,BM= AM,
又∵BC=BM+CM, AM=AC+CM,
∴BC-AC= BM+MC-AC= AM+MC-AC= AC+CM+MC-AC=2CM=2;
(3)![]() =-(x-1)2+4,
=-(x-1)2+4,
所以平移后的抛物线解析式为: ![]() -4=-x2+2x-1,
-4=-x2+2x-1,
设P(m,-m2+2m+3),则平移后对应点Q(m,-m2+2m-1),
因为OP=OQ,所以P、Q两点关于x轴对称,
所以:(-m2+2m+3)+(-m2+2m-1)=0,
解得:m1=![]() ,m2=
,m2=![]() ,
,
所以:点Q的坐标为(![]() )或(
)或(![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,点D为AB的中点,过点D作DE∥BC交AC于E.
(1)求证:E为AC的中点;
(2)如图2,过点D作QD⊥AB交BC的延长线于Q,过点E作EP⊥AC交CB的延长线于P,连AP、AQ.若PQ=12,AP+AQ=20,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.

(1)试问坡AB的高BT为多少米?
(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米, ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
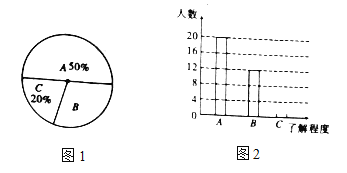
【题目】为传播奥运知识,小刚就本班学生对奥运知识的了解程度进行了一次调查统计:A:熟悉,B:了解较多,C:一般了解图1和图2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求该班共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)如果全年级共1000名同学,请你估算全年级对奥运知识“了解较多”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点![]() ,点
,点![]() 第一次跳动至点
第一次跳动至点![]() ,第二次点
,第二次点![]() 跳动至点
跳动至点![]() ,第三次点
,第三次点![]() 跳动至点
跳动至点![]() ,第四次点
,第四次点![]() 跳动至点
跳动至点![]() ,……依此规律跳动下去,则点
,……依此规律跳动下去,则点![]() 与点
与点![]() 之间的距离是( )
之间的距离是( )

A. 2021B. 2020C. 2019D. 2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在前面学习中,一些乘法公式可以通过几何图形来进行验证,请结合下列两组图形回答问题:

图①说明:左侧图形中阴影部分由右侧阴影部分分割后拼接而成.
图②说明:边长为![]() 的正方形的面积分割成如图所示的四部分.
的正方形的面积分割成如图所示的四部分.
(1)请结合图①和图②分别写出学过的两个乘法公式:
图①:____________,图②:____________;
(2)请利用上面的乘法公式计算:
①![]() ;
;
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.
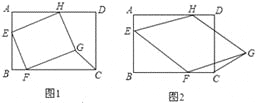
(1)如图①,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用a表示);
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某股民上星期五买进某公司股票1000 股,每股27 元,下表为本周内每日该股票的涨跌情况(单位:元.注:股市周六和周日不开市)

(1) 星期三收盘时,每股多少元?
(2) 本周内每股最高价的多少元?最低价是多少元?
(3) 已知该股民买进股票时需付![]() 的手续费,卖出时要付成交额
的手续费,卖出时要付成交额![]() 的手续费和
的手续费和![]() 的交易税.他一直观望到星期五才将股票全部卖出,请算算他本周的收益如何?
的交易税.他一直观望到星期五才将股票全部卖出,请算算他本周的收益如何?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com