
【题目】已知:在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.
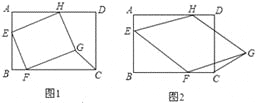
(1)如图①,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用a表示);
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
【答案】(1)10;(2)12-a;(3)不能
【解析】解:(1)过点G作GM⊥BC于M.在正方形EFGH中,
∠HEF=90°,EH=EF,
∴∠AEH+∠BEF=90°.
∵∠AEH+∠AHE=90°,
∴∠AHE=∠BEF.
又∵∠A=∠B=90°,
∴△AHE≌△BEF.
同理可证△MFG≌△BEF.
∴GM=BF=AE=2.∴FC=BC-BF=10.
∴![]() .
.
(2)过点G作GM⊥BC交BC的延长线于M,连接HF.
∵AD∥BC,∴∠AHF=∠MFH.
∵EH∥FG,∴∠EHF=∠GFH.
∴∠AHE=∠MFG.
又∵∠A=∠GMF=90°,EH=GF,
∴△AHE≌△MFG.∴GM=AE=2.
∴![]() .
.
(3)△GFC的面积不能等于2.
说明一:∵若S△GFC=2,则12-a=2,∴a=10.
此时,在△BEF中,
![]() .
.
在△AHE中,
![]() ,
,
∴AH>AD,即点H已经不在边AD上,故不可能有S△GFC=2.
说明二:△GFC的面积不能等于2.∵点H在AD上,
∴菱形边EH的最大值为![]() ,∴BF的最大值为
,∴BF的最大值为![]() .
.
又∵函数S△GFC=12-a的值随着a的增大而减小,
∴S△GFC的最小值为![]() .
.
又∵![]() ,∴△GFC的面积不能等于2.
,∴△GFC的面积不能等于2.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
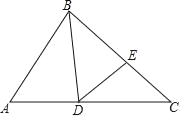
【题目】如图,BD是△ABC的角平分线,点E位于边BC上,已知BD是BA与BE的比例中项.
(1)求证:∠CDE=![]() ∠ABC;
∠ABC;
(2)求证:ADCD=ABCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点(2,3),对称轴为直线x =1.
经过点(2,3),对称轴为直线x =1.
(1)求抛物线的表达式;
(2)如果垂直于y轴的直线l与抛物线交于两点A(![]() ,
, ![]() ),B(
),B(![]() ,
, ![]() ),其中
),其中![]() ,
, ![]() ,与y轴交于点C,求BC
,与y轴交于点C,求BC![]() AC的值;
AC的值;
(3)将抛物线向上或向下平移,使新抛物线的顶点落在x轴上,原抛物线上一点P平移后对应点为点Q,如果OP=OQ,直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高速公路某收费站出城方向有编号为![]() 的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
收费出口编号 |
|
|
|
|
|
通过小客车数量(辆) | 260 | 330 | 300 | 360 | 240 |
在![]() 五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据图中提供的信息,有下列说法:

(1)他们都行驶了18千米;
(2)甲在途中停留了0.5小时;
(3)乙比甲晚出发了0.5小时;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙两人同时到达目的地
其中符合图象描述的说法有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() 且
且![]() ,延长
,延长![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,连接
,连接![]() 、
、![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 是等边三角形;③
是等边三角形;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中正确的有( )
;其中正确的有( )

A.![]() 个B.
个B.![]() 个
个
C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(1)求△OCD的面积;
(2)当BE=![]() AC时,求CE的长.
AC时,求CE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com