
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
【答案】(1) t=1或![]() ;(2)
;(2) ![]()
【解析】试题分析:
(1)由∠B是△BPQ与△ABC的公共角,可知,若两三角形相似,存在两种情况:①△BPQ∽△BAC;②△BPQ∽△BCA;分这两种情况结合相似三角形的性质和题意即可解得对应的t的值;
(2)如图1,过P作PM⊥BC于点M,AQ,CP交于点N,由题意可知:当AQ⊥CP时,△ACQ∽△CMP,由相似三角形的性质列出比例式即可解得对应的t的值.
试题解析:
(1)∵Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,
∴由勾股定理可得:BA=![]() ;
;
由题意现分两种情况讨论:
①当△BPQ∽△BAC时, ![]() ,
,
∵BP=5t,QC=4t,AB=10,BC=8,
∴![]() ,解得:
,解得: ![]() ;
;
②当△BPQ∽△BCA时, ![]() ,
,
∴![]() ,解得,
,解得, ![]() ;
;
综上所述,当![]() 或
或![]() 时,△BPQ与△ABC相似.
时,△BPQ与△ABC相似.
(2)过P作PM⊥BC于点M,AQ,CP交于点N,如图1所示:

∴∠PMB=∠ACB=90°,
∴PM∥AC,
∴△BPM∽△BAC,
∴![]() ,即
,即![]() ,
,
∴PM=![]() ,BM=
,BM=![]() ,
,
∴CM=![]() .
.
∵AQ⊥CP,∠ACB=90°,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
∵∠ACQ=∠PMC,
∴△ACQ∽△CMP,
∴![]() ,即
,即![]() ,解得
,解得![]() .
.


科目:初中数学 来源: 题型:
【题目】列分式方程解应用题:
某学校准备组织部分学生到少年宫参加活动,陈老师从少年宫带回来两条信息:
信息一:按原来报名参加的人数,共需要交费用320元,如果参加的人数能够增加到原来人数的2倍,就可以享受优惠,此时只需交费用480元;
信息二:如果能享受优惠,那么参加活动的每位同学平均分摊的费用比原来少4元.
根据以上信息,原来报名参加的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点![]() ,点
,点![]() 第一次跳动至点
第一次跳动至点![]() ,第二次点
,第二次点![]() 跳动至点
跳动至点![]() ,第三次点
,第三次点![]() 跳动至点
跳动至点![]() ,第四次点
,第四次点![]() 跳动至点
跳动至点![]() ,……依此规律跳动下去,则点
,……依此规律跳动下去,则点![]() 与点
与点![]() 之间的距离是( )
之间的距离是( )

A. 2021B. 2020C. 2019D. 2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在前面学习中,一些乘法公式可以通过几何图形来进行验证,请结合下列两组图形回答问题:

图①说明:左侧图形中阴影部分由右侧阴影部分分割后拼接而成.
图②说明:边长为![]() 的正方形的面积分割成如图所示的四部分.
的正方形的面积分割成如图所示的四部分.
(1)请结合图①和图②分别写出学过的两个乘法公式:
图①:____________,图②:____________;
(2)请利用上面的乘法公式计算:
①![]() ;
;
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.
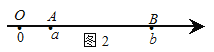
当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
![]()
当A、B两点都不在原点时,如图2,点A、B都在原点的右边
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=![]() =∣a-b∣;
=∣a-b∣;
如图3,当点A、B都在原点的左边,
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=![]() =∣a-b∣;
=∣a-b∣;
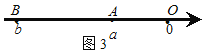
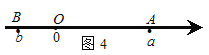
如图4,当点A、B在原点的两边,
∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= ![]() =∣a-b∣;
=∣a-b∣;
回答下列问题:
(1)数轴上表示1和6的两点之间的距离是 ,数轴上表示2和-3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是-4,则点A和B之间的距离是 ,若∣AB∣=3,那么x为 ;
(3)当x是 时,代数式![]() ;
;
(4)若点A表示的数![]() ,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒
,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒![]() 个单位长度,求运动几秒后,点Q与点P 相距1个单位?(请写出必要的求解过程)
个单位长度,求运动几秒后,点Q与点P 相距1个单位?(请写出必要的求解过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.
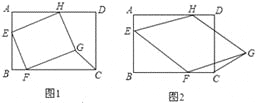
(1)如图①,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用a表示);
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,连接MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为( )

A.28°B.56°C.62°D.72°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,分别过点
,分别过点![]() 、
、![]() 向直线
向直线![]() 作垂线,垂足分别为
作垂线,垂足分别为![]() 、
、![]() .
.

(1)如图1,当点![]() ,
,![]() 位于直线
位于直线![]() 的同侧时,证明:
的同侧时,证明:![]() .
.
(2)如图2,若点![]() ,
,![]() 在直线
在直线![]() 的异侧,其它条件不变,
的异侧,其它条件不变,![]() 是否依然成立?请说明理由.
是否依然成立?请说明理由.
(3)图形变式:如图3,锐角![]() 中,
中,![]() ,直线
,直线![]() 经过点
经过点![]() ,点
,点![]() ,
,![]() 分别在直线
分别在直线![]() 上,点
上,点![]() ,
,![]() 位于
位于![]() 的同一侧,如果
的同一侧,如果![]() ,请找到图中的全等三角形,并直接写出线段
,请找到图中的全等三角形,并直接写出线段![]() ,
,![]() ,
,![]() 的数量关系.
的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com