
【题目】已知![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,分别过点
,分别过点![]() 、
、![]() 向直线
向直线![]() 作垂线,垂足分别为
作垂线,垂足分别为![]() 、
、![]() .
.

(1)如图1,当点![]() ,
,![]() 位于直线
位于直线![]() 的同侧时,证明:
的同侧时,证明:![]() .
.
(2)如图2,若点![]() ,
,![]() 在直线
在直线![]() 的异侧,其它条件不变,
的异侧,其它条件不变,![]() 是否依然成立?请说明理由.
是否依然成立?请说明理由.
(3)图形变式:如图3,锐角![]() 中,
中,![]() ,直线
,直线![]() 经过点
经过点![]() ,点
,点![]() ,
,![]() 分别在直线
分别在直线![]() 上,点
上,点![]() ,
,![]() 位于
位于![]() 的同一侧,如果
的同一侧,如果![]() ,请找到图中的全等三角形,并直接写出线段
,请找到图中的全等三角形,并直接写出线段![]() ,
,![]() ,
,![]() 的数量关系.
的数量关系.
【答案】(1)详见解析;(2)详见解析;(3)![]() ,
,![]() .
.
【解析】
(1)易证∠ABD=∠CAE,由AAS即可得出△ABD≌△CAE;
(2)易证∠ABD=∠CAE,由AAS即可得出△ABD≌△CAE;
(3)由∠CEA=∠ADB=∠BAC,根据三角形内角和定理和平角的定义可得∠ECA+∠EAC=∠EAC+∠DAB,得出∠DAB=∠ECA,由AAS即可证得△ABD≌△CAE,得出AD=EC,DB=AE,则ED=EC+DB.
解:(1)在![]() 中,
中,![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() .
.
(2)在![]() 中,
中,![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
(3)![]() ,
,![]() .
.
理由如下:
∵∠CEA=∠ADB=∠BAC,
∴∠ECA+∠EAC=∠EAC+∠DAB,
∴∠DAB=∠ECA,
在△ABD和△CAE中,
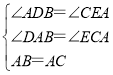
∴△ABD≌△CAE(AAS),
∴AD=EC,DB=AE,
∴ED=AD+AE=EC+DB.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() 且
且![]() ,延长
,延长![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,连接
,连接![]() 、
、![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 是等边三角形;③
是等边三角形;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中正确的有( )
;其中正确的有( )

A.![]() 个B.
个B.![]() 个
个
C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y1=x与反比例函数y2=![]() 的图像交于A、C两点,AB⊥x轴,垂足为B, CD⊥x轴,垂足为D.给出下列结论:①四边形ABCD是平行四边形,其面积为18;②AC=3
的图像交于A、C两点,AB⊥x轴,垂足为B, CD⊥x轴,垂足为D.给出下列结论:①四边形ABCD是平行四边形,其面积为18;②AC=3![]() ;③当-3≤x<0或x≥3时,y1≥y2;④当x逐渐增大时,y1随x的增大而增大,y2随x的增大而减小.其中正确的结论有( )
;③当-3≤x<0或x≥3时,y1≥y2;④当x逐渐增大时,y1随x的增大而增大,y2随x的增大而减小.其中正确的结论有( )

A.①④B.①③④C.①③D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(1)求△OCD的面积;
(2)当BE=![]() AC时,求CE的长.
AC时,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年十一黄金周商场大促销,某店主计划从厂家采购高级羽绒服和时尚皮衣两种产品共20件,高级羽绒服的采购单价y1(元/件)与采购数量x1(件)满足y1=﹣20x1+1500(0<x1≤20,x1为整数);时尚皮衣的采购单价y2(元/件)与采购数量x2(件)满足y2=﹣10x2+1300(0<x2≤20,x2为整数).
(1)经店主与厂家协商,采购高级羽绒服的数量不少于时尚皮衣数量,且高级羽绒服采购单价不低于1240元,问该店主共有几种进货方案?
(2)该店主分别以1760元/件和1700元/件的销售出高级羽绒服和时尚皮衣,且全部售完,则在(1)问的条件下,采购高级羽绒服多少件时总利润最大?并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水池有若干个进水口与出水口,每个口进出水的速度如图1、图2所示,只开1个进水口持续15小时可将水池注满.

(1)某段时间内蓄水量V(m3)与时间t(h)的关系如图3所示,0~3时只开2个进水口,3~b时只开1个进水口与1个出水口,9~c只开1个出水口,求证:a=b+c.
(2)若同时开2个出水口与1个进水口,多久可将满池的水排完?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com