
【题目】如图,在平行四边形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() 且
且![]() ,延长
,延长![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,连接
,连接![]() 、
、![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 是等边三角形;③
是等边三角形;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中正确的有( )
;其中正确的有( )

A.![]() 个B.
个B.![]() 个
个
C.![]() 个D.
个D.![]() 个
个
【答案】B
【解析】
由平行四边形的性质和角平分线的定义得出∠BAE=∠BEA,得出AB=BE=AE,得出②正确;由△ABE是等边三角形得出∠ABE=∠EAD=60°,由SAS证明△ABC≌△EAD,得出①正确;由S△AEC=S△DEC,S△ABE=S△CEF得出⑤正确;③和④不正确.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EAD=∠AEB,
又∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形;②正确;
∴∠ABE=∠EAD=60°,
在△ABC和△EAD中,
 ,
,
∴△ABC≌△EAD(SAS);①正确;
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),
∴S△FCD=S△ABC,
又∵△AEC与△DEC同底等高,
∴S△AEC=S△DEC,
∴S△ABE=S△CEF;⑤正确.
若AD与BF相等,则BF=BC,
题中未限定这一条件,
∴③不一定正确;
若S△BEF=S△ACD;则S△BEF=S△ABC,
则AB=BF,
∴BF=BE,题中未限定这一条件,
∴④不一定正确;
正确的有①②⑤.
故选:B.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】已知:在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.
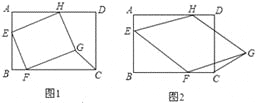
(1)如图①,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用a表示);
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,连接MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为( )

A.28°B.56°C.62°D.72°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h) | 0 | 1 | 2 | 3 | … |
油箱剩余油量Q(L) | 100 | 94 | 88 | 82 | … |
①根据上表的数据,请你写出Q与t的关系式;
②汽车行驶5h后,油箱中的剩余油量是多少?
③该品牌汽车的油箱加满50L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某股民上星期五买进某公司股票1000 股,每股27 元,下表为本周内每日该股票的涨跌情况(单位:元.注:股市周六和周日不开市)

(1) 星期三收盘时,每股多少元?
(2) 本周内每股最高价的多少元?最低价是多少元?
(3) 已知该股民买进股票时需付![]() 的手续费,卖出时要付成交额
的手续费,卖出时要付成交额![]() 的手续费和
的手续费和![]() 的交易税.他一直观望到星期五才将股票全部卖出,请算算他本周的收益如何?
的交易税.他一直观望到星期五才将股票全部卖出,请算算他本周的收益如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,分别过点
,分别过点![]() 、
、![]() 向直线
向直线![]() 作垂线,垂足分别为
作垂线,垂足分别为![]() 、
、![]() .
.

(1)如图1,当点![]() ,
,![]() 位于直线
位于直线![]() 的同侧时,证明:
的同侧时,证明:![]() .
.
(2)如图2,若点![]() ,
,![]() 在直线
在直线![]() 的异侧,其它条件不变,
的异侧,其它条件不变,![]() 是否依然成立?请说明理由.
是否依然成立?请说明理由.
(3)图形变式:如图3,锐角![]() 中,
中,![]() ,直线
,直线![]() 经过点
经过点![]() ,点
,点![]() ,
,![]() 分别在直线
分别在直线![]() 上,点
上,点![]() ,
,![]() 位于
位于![]() 的同一侧,如果
的同一侧,如果![]() ,请找到图中的全等三角形,并直接写出线段
,请找到图中的全等三角形,并直接写出线段![]() ,
,![]() ,
,![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=4,AD=3,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.
(1)若点P落在矩形ABCD的边AB上(如图1).
①当点P与点A重合时,∠DEF= °,当点E与点A重合时,∠DEF= °.
②当点E在AB上时,点F在DC上时(如图2),若AP=![]() ,求四边形EPFD的周长.
,求四边形EPFD的周长.
(2)若点F与点C重合,点E在AD上,线段BA与线段FP交于点M(如图3),当AM=DE时,请求出线段AE的长度.

(3)若点P落在矩形的内部(如图4),且点E、F分别在AD、DC边上,请直接写出AP的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com