
【题目】过正方形![]() (四边都相等,四个角都是直角)的顶点
(四边都相等,四个角都是直角)的顶点![]() 作一条直线
作一条直线![]() .
.
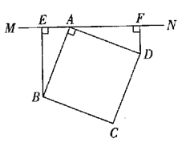
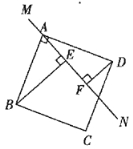
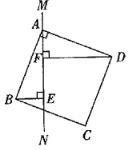
图(1) 图(2) 图(3)
(1)当![]() 不与正方形任何一边相交时,过点
不与正方形任何一边相交时,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() 如图(1),请写出
如图(1),请写出![]() ,
,![]() ,
,![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
(2)若改变直线![]() 的位置,使
的位置,使![]() 与
与![]() 边相交如图(2),其它条件不变,
边相交如图(2),其它条件不变,![]() ,
,![]() ,
,![]() 的关系会发生变化,请直接写出
的关系会发生变化,请直接写出![]() ,
,![]() ,
,![]() 的数量关系,不必证明;
的数量关系,不必证明;
(3)若继续改变直线![]() 的位置,使
的位置,使![]() 与
与![]() 边相交如图(3),其它条件不变,
边相交如图(3),其它条件不变,![]() ,
,![]() ,
,![]() 的关系又会发生变化,请直接写出
的关系又会发生变化,请直接写出![]() ,
,![]() ,
,![]() 的数量关系,不必证明.
的数量关系,不必证明.
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC﹣AB=2BE中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x的函数y=(5m-3)x2-n+(m+n).
(1)当m,n为何值时,函数是一次函数?
(2)当m,n为何值时,函数是正比例函数?
(3)当m,n为何值时,函数是反比例函数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形AOBC中,对角线交于点E,双曲线y=![]() (k>0)经过A、E两点,若AC : OB = 1:3,梯形AOBC面积为24,则k =( )
(k>0)经过A、E两点,若AC : OB = 1:3,梯形AOBC面积为24,则k =( )
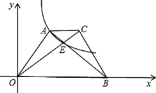
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,假分数可以化为整数与真分数的和的形式.例如:![]() ,在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像
,在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像![]() ,
,![]() ,这样的分式是假分式;像
,这样的分式是假分式;像![]() ,
,![]() ,这样的分式是真分式.类似的,假分式也可以化为整数与真分式的和的形式.
,这样的分式是真分式.类似的,假分式也可以化为整数与真分式的和的形式.
例如:![]() ;
;
![]() ;
;
或![]()
(1)分式![]() 是 分式(填“真”或“假”)
是 分式(填“真”或“假”)
(2)将分式![]() 化为整式与真分式的和的形式;
化为整式与真分式的和的形式;
(3)如果分式![]() 的值为整数,求
的值为整数,求![]() 的整数值.
的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
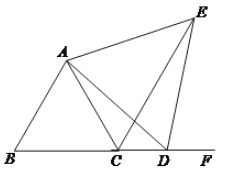
【题目】如图, △ABC是等边三角形,D是BC延长线上任意一点,以AD为一边向右侧作等边△ADE,连接CE.
1.求证:△CAE≌△BAD;
2.判断直线AB与EC的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com