
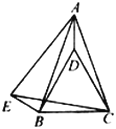
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 内,
内,![]() ,
,![]() ,点
,点![]() 在
在![]() 外,
外,![]() ,
,![]() .
.
(1)求![]() 的度数.
的度数.
(2)判断![]() 的形状并加以证明.
的形状并加以证明.
(3)连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)∠ADC=150°;(2)△ACE是等边三角形,证明见解析;(3)DE=6.
【解析】
(1)先证明△DBC是等边三角形,根据SSS证得△ADC≌△ADB,得到∠ADC=∠ADB即可得到答案;
(2)证明△ACD≌△ECB得到AC=EC,利用![]() 即可证得
即可证得![]() 的形状;
的形状;
(3)根据![]() 及等边三角形的性质求出∠EDB=30°,利用
及等边三角形的性质求出∠EDB=30°,利用![]() 求出∠DBE=90°,根据△ACD≌△ECB,AD=3,即可求出DE的长.
求出∠DBE=90°,根据△ACD≌△ECB,AD=3,即可求出DE的长.
(1)∵BD=BC,∠DBC=60°,
∴△DBC是等边三角形.
∴DB=DC,∠BDC=∠DBC=∠DCB=60°.
在△ADB和△ADC中,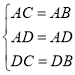 ,
,
∴△ADC≌△ADB.
∴∠ADC=∠ADB.
∴∠ADC=![]() (360°﹣60°)=150°.
(360°﹣60°)=150°.
(2)△ACE是等边三角形.
理由如下:∵∠ACE=∠DCB =60°,
∴∠ACD=∠ECB.
∵∠CBE=150°,∠ADC=150°
∴∠ADC=∠EBC.
在△ACD和△ECB中, ,
,
∴△ACD≌△ECB.
∴AC=CE.
∵∠ACE=60°,
∴△ACE是等边三角形.
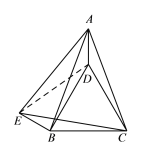
(3)连接DE.
∵DE⊥CD,
∴∠EDC=90°.
∵∠BDC=60°,
∴∠EDB=30°.
∵∠CBE=150°,∠DBC=60°,∴∠DBE=90°.
∴EB=![]() DE.
DE.
∵△ACD≌△ECB,AD=3,
∴EB = AD =3.
∴DE=2EB=6.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
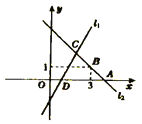
【题目】如图直线![]() 对应的函数表达式为
对应的函数表达式为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .直线
.直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
(1)求点![]() ,点
,点![]() 的坐标;
的坐标;
(2)求直线![]() 对应的函数表达式;
对应的函数表达式;
(3)求![]() 的面积;
的面积;
(4)利用函数图象写出关于![]() ,
,![]() 的二元一次方程组
的二元一次方程组![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°,BD、CE分别是△ABC、△BCD的角平分线.则图中的等腰三角形有( )

A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,以AB为直径作⊙O恰好与CD相切.
(1)求证:AD+BC=CD;
(2)若E为OA的中点,连结CE并延长交DA的延长线于F,当AE=AF时,求sin∠DCF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料:我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、十字相乘法等等,其中十字相乘法在高中应用较多.
十字相乘法:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图),如:将式子![]() 和
和![]() 分解因式,如图:
分解因式,如图:
![]() ;
;
![]() .
.
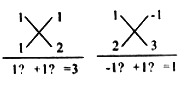
请你仿照以上方法,探索解决下列问题:
(1)分解因式:![]() ;
;
(2)分解因式:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里有4排日光灯,每排灯各由一个开关控制,但灯的排数序号与开关序号不一定对应,其中控制第二排灯的开关已坏(闭合开关时灯也不亮).
(1)将4个开关都闭合时,教室里所有灯都亮起的概率是 ;
(2)在4个开关都闭合的情况下,不知情的雷老师准备做光学实验,由于灯光太强,他需要关掉部分灯,于是随机将4个开关中的2个断开,请用列表或画树状图的方法,求恰好关掉第一排与第三排灯的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的转盘,分成三个相同的扇形,指针位置固定转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,当作指向右边的扇形).
(1)求事件“转动一次,得到的数恰好是0”发生的概率;
(2)写出此情景下一个不可能发生的事件.
(3)用树状图或列表法,求事件“转动两次,第一次得到的数与第二次得到的数绝对值相等”发生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大石桥市政府为了落实“暖冬惠民工程”,计划对城区内某小区的部分老旧房屋及供暖管道和部分路段的人行地砖、绿化带等公共设施进行全面更新改造。该工程乙队单独完成所需天数是甲队单独完成所需天数的1.5倍 , 若甲队先做10天,剩下两队合作30天完成。
(1)甲乙两个队单独完成此项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙对每天的施工费用为5.6万元,工程施工的预算费用为500万元,为了缩短工期并高效完成工程,拟预算的费用是否够用?若不够用,需追加预算多少万元?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
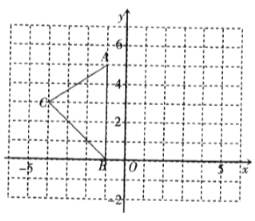
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 、
、![]() .
.
(1)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() (其中
(其中![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的对应点)并直接写出
的对应点)并直接写出![]() 点的坐标为 .
点的坐标为 .
(2)若直线![]() 经过点
经过点![]() 且与
且与![]() 轴平行,则点
轴平行,则点![]() 关于直线
关于直线![]() 的对称点的坐标为 .
的对称点的坐标为 .
(3)在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 最大,则点
最大,则点![]() 的坐标为 .
的坐标为 .
(4)第一象限有一点![]() ,在
,在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最短,画出最短路径,保留作图迹.
最短,画出最短路径,保留作图迹.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com