
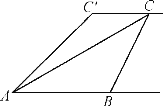
【题目】如图所示,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100 m.当气球沿与BA平行地方向飘移10 s后到达C′处时,在A处测得气球的仰角为45°.
(1)求气球的高度(保留根式);
(2)求气球飘移的平均速度(保留根式).
【答案】(1)CD=50![]() m.(2)(15-5
m.(2)(15-5![]() ) m/s.
) m/s.
【解析】
(1)分别过C、C′作AB的垂线,设垂足为D、E;在Rt△ACD和Rt△BCD中,利用所给角的三角函数分别用BD表示出CD,联立两式即可求出CD、BD的长.
(2)直角梯形ADCC′中,已知了BD、AB的长,即可求出AD的长;而AE的长可在Rt△AEC′中利用已知角的三角函数求出,即可得出ED、CC′的长,也就得出了气球10秒漂移的距离,根据速度=路程÷时间,即可得解.
解:(1)如答图所示,作CD⊥AB,C′E⊥AB,垂足分别为D,E.
∵CD=BD·tan60°,CD=(100+BD)·tan30°,
∴(100+BD)·tan30°=BD·tan60°,
∴BD=50(m),CD=50![]() (m),
(m),
∴气球的高度约为CD=50![]() m.
m.
(2)∵BD=50 m,AB=100 m,
∴AD=150 m,
又∵AE=C′E=50![]() m,
m,
∴DE=(150-50![]() )m,
)m,
(150-50![]() )÷10=(15-5
)÷10=(15-5![]() )(m/s).
)(m/s).
∴气球飘移的平均速度约为(15-5![]() ) m/s.
) m/s.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
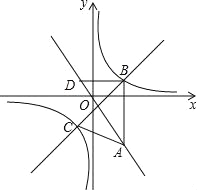
【题目】如图,在平面直角坐标系xOy中,点A(a,﹣![]() )在直线y=﹣
)在直线y=﹣![]() 上,AB∥y轴,且点B的纵坐标为1,双曲线y=
上,AB∥y轴,且点B的纵坐标为1,双曲线y=![]() 经过点B.
经过点B.
(1)求a的值及双曲线y=![]() 的解析式;
的解析式;
(2)经过点B的直线与双曲线y=![]() 的另一个交点为点C,且△ABC的面积为
的另一个交点为点C,且△ABC的面积为![]() .
.
①求直线BC的解析式;
②过点B作BD∥x轴交直线y=﹣![]() 于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
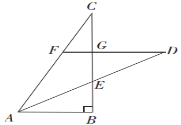
【题目】如图,在△ABC中,∠ABC=90°,且BC=6,AB=3,AD是∠BAC的平分线,与BC相交于点E,点G是BC上一点,E为线段BG的中点,DG⊥BC于点G,交AC于点F,则FG的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
科目:初中数学 来源: 题型:
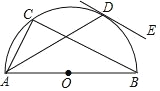
【题目】如图,△ABC 内接于半⊙O,AB 为直径,弦 AD 平分∠CAB,DE 切⊙O 于点 D.
(1) 求证:DE∥BC
(2) 若 AD=BC,⊙O 半径为 2,求∠CAD 与弧CD围成区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如表:
周数x | 1 | 2 | 3 | 4 |
价格y(元/千克) | 2 | 2.2 | 2.4 | 2.6 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式;
(2)进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的2.4元/千克,且y与周数x的变化情况满足二次函数y=﹣![]() x2+bx+c,请求出5月份y与x的函数关系式;
x2+bx+c,请求出5月份y与x的函数关系式;
(3)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=![]() x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=﹣
x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=﹣![]() x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
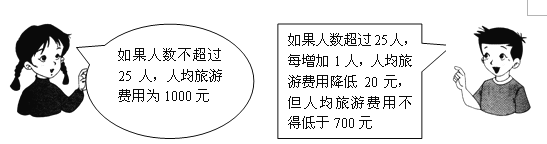 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com