
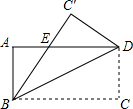
 如图,矩形ABCD沿直线BD折叠,使点C落在点C处,BC交AD于点E,AD=8,AB=4,则BE的长为( )
如图,矩形ABCD沿直线BD折叠,使点C落在点C处,BC交AD于点E,AD=8,AB=4,则BE的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 2$\sqrt{3}$ |
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
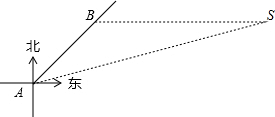 如图,一艘向东北方向航行的船,在A处观测灯塔S在船的北偏东67.5°的方向,航行6海里后到达B处,这时灯塔S恰好在船的正东方向.已知距离此灯塔8海里以外的海区为航行安全区域,这艘船可以继续沿东北方向航行吗?为什么?(参考数据:tan22.5°≈$\frac{2}{5}$;sin22.5°≈$\frac{19}{50}$;cos22.5°≈$\frac{23}{25}$)
如图,一艘向东北方向航行的船,在A处观测灯塔S在船的北偏东67.5°的方向,航行6海里后到达B处,这时灯塔S恰好在船的正东方向.已知距离此灯塔8海里以外的海区为航行安全区域,这艘船可以继续沿东北方向航行吗?为什么?(参考数据:tan22.5°≈$\frac{2}{5}$;sin22.5°≈$\frac{19}{50}$;cos22.5°≈$\frac{23}{25}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,-9) | B. | (-6,-1) | C. | (1,-2) | D. | (1,-8) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
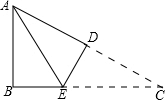 如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )
如图,在Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC沿DE折叠,使点C与点A重合,则AE的长等于( )| A. | 4cm | B. | $\frac{3}{2}$cm | C. | $\frac{25}{8}$cm | D. | $\frac{7}{2}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com