
【题目】用反证法证明:若二次方程8x2﹣(k﹣1)x+k﹣7=0有两个不等实数根,则两根不可能互为倒数.
【答案】证明:假设若二次方程8x2﹣(k﹣1)x+k﹣7=0有两个不等实数根,且两根互为倒数,
设两根为x1 , x2 , 由题意可得:x1x2=![]() =1,
=1,
解得:k=15,
故8x2﹣(15﹣1)x+18﹣7=0
即4x2﹣7x+4=0
则b2﹣4ac=49﹣64=﹣15<0,
此方程无实数根,故假设不成立,原命题正确,
即若二次方程8x2﹣(k﹣1)x+k﹣7=0有两个不等实数根,则两根不可能互为倒数.
【解析】首先假设若二次方程8x2﹣(k﹣1)x+k﹣7=0有两个不等实数根,且两根互为倒数,进而利用根与系数的关系得出k的值,再利用根的判别式得出矛盾,问题得证.
【考点精析】掌握求根公式和反证法是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;先假设命题中的结论不成立,然后由此经过推理,引出矛盾,判定所做的假设不正确,从而得到原命题成立,这种证明方法叫做反证法.


科目:初中数学 来源: 题型:
【题目】王师傅手中拿着一根长12cm的木条,则该木条不能与下列所给木条组成直角三角形的是( )
A. 5cm和13cm B. 9cm和15cm C. 16cm和20cm D. 9cm和13cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了奖励初三优秀毕业生,计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑比购买3台学习机多600元,购买2台平板电脑和3台学习机共需8400元.
(1)求购买1台平板电脑和1台学习机各需多少元?
(2)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过168000元,且购买学习机的台数不超过购买平板电脑台数的1.7倍.请问有哪几种购买方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.
(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的![]() ,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果方程x2+px+q=0的两个根是x1 , x2 , 那么x1+x2=﹣p,x1x2=q,请根据以上结论,解决下列问题:
(1)若p=﹣4,q=3,求方程x2+px+q=0的两根.
(2)已知实数a、b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,求 ![]() +
+ ![]() 的值;
的值;
(3)已知关于x的方程x2+mx+n=0,(n≠0),求出一个一元二次方程,使它的两个根分别是已知方程两根的倒数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等社团活动项目(每人只限一项)的情况,并将所得数据进行了统计,结果如图所示.![]()
![]()
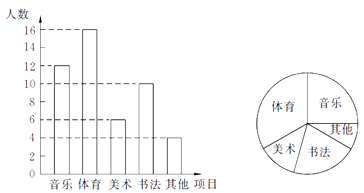
(1)在这次调查中,一共抽查了多少名学生?
(2)求出扇形统计图中参加“音乐”活动项目在扇形统计图中所对扇形圆心角的度数.
(3)若该校有2 400名学生,请估计该校参加“美术”活动项目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴l上,一动点Q从原点O出发,沿直线l以每秒钟2个单位长度的速度来回移动,其移动方式是先向右移动1个单位长度,再向左移动2个单位长度,又向右移动3个单位长度,再向左移动4个单位长度,又向右移动5个单位长度…![]()
(1)求出5秒钟后动点Q所处的位置;
(2)如果在数轴l上还有一个定点A,且A与原点O相距20个单位长度,问:动点Q从原点出发,可能与点A重合吗?若能,则第一次与点A重合需多长时间?若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com