
����Ŀ��ѧУΪ�˽������������ҵ�����ƻ�����һ��ƽ����Ժ�һ��ѧϰ������Ͷ�꣬����1̨ƽ����Աȹ���3̨ѧϰ����600Ԫ������2̨ƽ����Ժ�3̨ѧϰ������8400Ԫ��
��1������1̨ƽ����Ժ�1̨ѧϰ���������Ԫ��
��2��ѧУ����ʵ���������������ƽ����Ժ�ѧϰ����100̨��Ҫ������ܷ��ò�����168000Ԫ���ҹ���ѧϰ����̨������������ƽ�����̨����1.7�����������ļ��ֹ��������ַ�����ʡǮ��
���𰸡���1������1̨ƽ�������3000Ԫ������1̨ѧϰ����800Ԫ����2������1������ƽ�����38̨��ѧϰ��62̨������2������ƽ�����39̨��ѧϰ��61̨������3������ƽ�����40̨��ѧϰ��60̨������1��ʡǮ��
��������
�����������1���蹺��1̨ƽ�������xԪ������1̨ѧϰ����yԪ���������г������飬���������Ľ�õ�x��y��ֵ�����ɵõ������
��2���蹺��ƽ�����x̨��ѧϰ����100��x��̨�����ݡ�������ܷ��ò�����168000Ԫ���ҹ���ѧϰ����̨������������ƽ�����̨����1.7�����г�����ʽ�飬����⼯�����ɵó������������ó���ʡǮ�ķ�����
�����������1���蹺��1̨ƽ�������xԪ������1̨ѧϰ����yԪ����������ã�![]() ����ã�
����ã�![]() ��
��
������1̨ƽ�������3000Ԫ������1̨ѧϰ����800Ԫ��
��2���蹺��ƽ�����x̨��ѧϰ����100��x��̨��
��������ã�![]() ����ã�37.03��x��40��������x��ֵΪ38��39��40����x=38ʱ��y=62��x=39ʱ��y=61��x=40ʱ��y=60��
����ã�37.03��x��40��������x��ֵΪ38��39��40����x=38ʱ��y=62��x=39ʱ��y=61��x=40ʱ��y=60��
����1������ƽ�����38̨��ѧϰ��62̨������Ϊ114000+49600=163600��Ԫ����
����2������ƽ�����39̨��ѧϰ��61̨������Ϊ117000+48800=165800��Ԫ����
����3������ƽ�����40̨��ѧϰ��60̨������Ϊ120000+48000=168000��Ԫ����
��1��ʡǮ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼��DZ�Ȼ�¼����ǣ�������
A.ij��������100��B.̫����������ɽ
C.a2+b2����1D.����һ�Ų�Ʊ���н�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˹᳹��ʵ��ί�и�����ġ�����ƶ������ijУ���ƶ���һϵ�й��ڰ��A��B��ƶ����ļƻ����־�����ij������152�����絽A��B������ֳ�����ô�С������15������ǡ����һ���������������磬��֪�����ִ�С�������ػ������ֱ�Ϊ12��/����8��/����������A��B������˷����±���

��1������15�����д�С��������������
��2���ְ�������10������ǰ��A�壬�������ǰ��B�壬��ǰ��A��Ĵ����Ϊx����ǰ��A��B�����ܷ���ΪyԪ�������y��x�ĺ�������ʽ��
��3���ڣ�2���������£�������A������粻����100�䣬����д��ʹ�ܷ������ٵĻ������䷽������������ٷ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����5��д�Ų�ͬ���ֵĿ�Ƭ���밴Ҫ������Ƭ��������и����⣺![]()
��1������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ�����ֵij˻������γ�ȡ�����ֵ�Ƕ���?���ҳ�ȡ��2�ſ�Ƭ���� �� �˻������ֵΪ ��
��2������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ���������������С����γ�ȡ����Сֵ�Ƕ���?���ҳ�ȡ��2�ſ�Ƭ���� �� �̵���СֵΪ ��
��3������ȡ��4�ſ�Ƭ����ѧ�������㷽����ʹ���Ϊ24����γ�ȡ��д������ʽ�ӡ���д��һ�ּ��ɣ������ҳ�ȡ��4�ſ�Ƭ�������� ��
��24��ʽ��Ϊ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���x2��1�ĸ��ǣ�������
A.x1��x2��1B.x1��x2����1C.x1����1��x2��1D.��ʵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ����Ӱ뾶Ϊ 2 �ġ�O�ϵ� A0��������������� A0O �����˶�����O�ϵĵ� A1�������������������� A1O �н�Ϊ60��ķ����˶�����O�ϵĵ� A2���������ִ� A2��������������� A2O �����˶�����O�ϵĵ� A3�������������������� A3O �н�Ϊ60��ķ����˶�����O�ϵĵ� A4���������˹����˶����� A2017������� A2017��� A0��ľ�����( )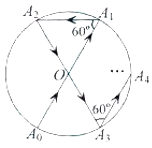
A.4
B.2
C.![]()
D.0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���÷�֤��֤���������η���8x2����k��1��x+k��7=0����������ʵ�����������������ܻ�Ϊ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ��
��1����ʽ��a1= ![]() =
= ![]() ��
�� ![]() ��
��
��2����ʽ��a2= ![]() =
= ![]() ����
���� ![]() ����
����
��3����ʽ��a3= ![]() =
= ![]() ����
���� ![]() ����
����
��4����ʽ��a4= ![]() =
= ![]() ����
���� ![]() ����
����
��
�����������⣺
��1�������Ϲ����г���5����ʽ��a5=��
��2���ú���n�Ĵ���ʽ��ʾ��n����ʽ��an==��nΪ����������
��3����a1+a2+a3+a4+��+a100��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com