Question

已知：如图，在△ABC中，AB=AC，∠BAC=30°．点D为△ABC内一点，

且DB=DC，∠DCB=30°．点E为BD延长线上一点，且AE=AB

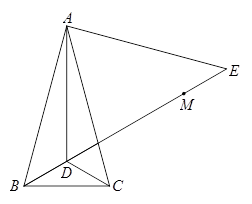
1.求∠ADE的度数

2.若点M在DE上，且DM=DA，

求证：ME=DC．

 

Answer 1

 

1.60°

2.

解析:（1）如图4．

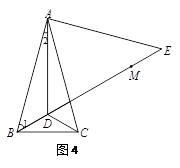
∵△ABC中，AB=AC，∠BAC=30°，

∴∠ABC=∠ACB==75°．

∵DB=DC，∠DCB=30°，

∴∠DBC=∠DCB=30°．

∴∠1=∠ABC－∠DBC=75°－30°=45°．

∵AB=AC，DB=DC，

∴AD所在直线垂直平分BC．

∴AD平分∠BAC．

∴∠2=∠BAC==15°．   ∴∠ADE=∠1＋∠2=45°＋15°=60°． 

证明：（2）证法一：连接AM，取BE的中点N，连接AN．（如图5）

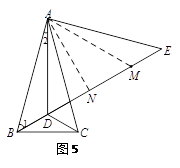
∵△ADM中，DM=DA，∠ADE=60°，

∴△ADM为等边三角形．   ∵△ABE中，AB=AE，N为BE的中点，

∴BN=NE，且AN⊥BE．

∴DN=NM．  

∴BN－DN =NE－NM，

即BD=ME．

∵DB=DC，

∴ME = DC．

证法二：连接AM．（如图6）

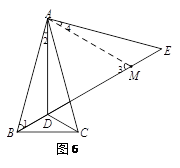
∵△ADM中，DM=DA，∠ADE=60°，

∴△ADM为等边三角形．

∴∠3=60°．

∵AE=AB，

∴∠E=∠1=45°．

∴∠4=∠3－∠E=60°－45°=15°．

∴∠2=∠4．

在△ABD和△AEM中，

             ∠1 =∠E，

             AB=AE，

             ∠2 =∠4，

∴△ABD≌△AEM．  

∴BD =EM．

∵DB = DC，

∴ME = DC．