
【题目】如图,分别过第二象限内的点![]() 作
作![]() 轴的平行线,与
轴的平行线,与![]() 轴分别交于点
轴分别交于点![]() 与双曲线
与双曲线![]() 分别交于点
分别交于点![]()
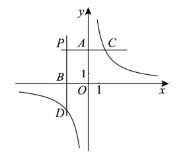
下面四个结论:
①存在无数个点![]() 使
使![]() ;
;
②存在无数个点![]() 使
使![]() ;
;
③至少存在一个点![]() 使
使![]() ;
;
④至少存在一个点![]() 使
使![]() .
.
所有正确结论的序号是________.
【答案】①②④
【解析】
如图,设C(m,![]() ),D(n,
),D(n,![]() ),则P(n,
),则P(n,![]() ),利用反比例函数k的几何意义得到S△AOC=3,S△BOD=3,则可对①进行判断;根据三角形面积公式可对②进行判断;通过计算S四边形OAPB和S△ACD得到m与n的关系可对对③进行判断.
),利用反比例函数k的几何意义得到S△AOC=3,S△BOD=3,则可对①进行判断;根据三角形面积公式可对②进行判断;通过计算S四边形OAPB和S△ACD得到m与n的关系可对对③进行判断.
解:如图,设C(m,![]() ),D(n,
),D(n,![]() ),则P(n,
),则P(n,![]() ),
),
∵S△AOC=![]() ,S△BOD=
,S△BOD=![]() ,
,
∴S△AOC=S△BOD;所以①正确;
∵S△POA=![]() ,S△POB=
,S△POB=![]() ,
,
∴S△POA=S△POB;所以②正确;
∵S△PCD=![]() ,
,
∴当![]() 时,即3m2+4mn+3n2=0,
时,即3m2+4mn+3n2=0,
∵△=42-4×3×3=-20<0,
∴不存在点![]() 使
使![]() ;所以③错误;
;所以③错误;
∵S四边形OAPB=﹣n×![]() ,S△ACD=
,S△ACD=![]() ,
,
∴当![]() 时,即m2﹣mn﹣2n2=0,
时,即m2﹣mn﹣2n2=0,
∴m=2n(舍去)或m=﹣n,此时P点为无数个,所以④正确.
故答案为:①②④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,将线段 AB 先向右平移 5 个单位,再将所得线段绕原点按顺时针方向旋转 90°,得到线段 AB ,则点 B 的对应点 B′的坐标是( )
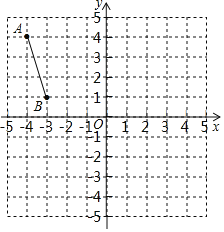
A.(-4 , 1)B.( -1, 2)C.(4 ,- 1)D.(1 ,- 2)
查看答案和解析>>
科目:初中数学 来源: 题型:
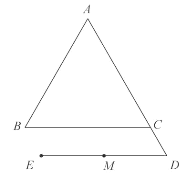
【题目】如图,在等边![]() 中,D为边AC的延长线上一点(
中,D为边AC的延长线上一点(![]() ),平移线段BC,使点C移动到点D,得到线段ED,M为ED的中点,过点M作ED的垂线,交BC于点F,交AC于点G.
),平移线段BC,使点C移动到点D,得到线段ED,M为ED的中点,过点M作ED的垂线,交BC于点F,交AC于点G.
(1)依题意补全图形;
(2)求证:![]() ;
;
(3)连接DF并延长交AB于点H,用等式表示线段AH与CG的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数![]() (
(![]() 为常数,
为常数,![]() )的图象过点
)的图象过点![]() 和点
和点![]() ,函数图象最低点
,函数图象最低点![]() 的纵坐标为
的纵坐标为![]() .直线
.直线![]() 的解析式为
的解析式为![]()
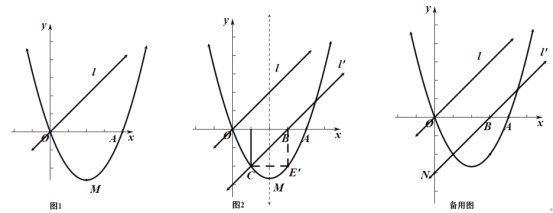
![]() 求二次函数的解析式;
求二次函数的解析式;
![]() 直线
直线![]() 沿
沿![]() 轴向右平移,得直线
轴向右平移,得直线![]() ,
,![]() 与线段
与线段![]() 相交于点
相交于点![]() ,与
,与![]() 轴下方的抛物线相交于点
轴下方的抛物线相交于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,把
,把![]() 沿直线
沿直线![]() 折叠,当点
折叠,当点![]() 恰好落在抛物线上点
恰好落在抛物线上点![]() 时(图
时(图![]() 求直线
求直线![]() 的解析式;
的解析式;
![]() 在
在![]() 的条件下,
的条件下,![]() 与
与![]() 轴交于点
轴交于点![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,P为
,P为![]() 上的动点,当
上的动点,当![]() 为等腰三角形时,求符合条件的点
为等腰三角形时,求符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
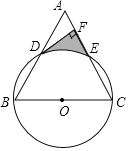
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,点
上,点![]() 是
是![]() 上一动点,且与点
上一动点,且与点![]() 分别位于直径
分别位于直径![]() 的两侧,
的两侧,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ;
;

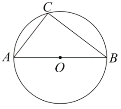
(1)当点![]() 运动到什么位置时,
运动到什么位置时,![]() 恰好是
恰好是![]() 的切线?画出图形并加以说明.
的切线?画出图形并加以说明.
(2)若点![]() 与点
与点![]() 关于直径
关于直径![]() 对称,且
对称,且![]() ,画出图形求此时
,画出图形求此时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.
(1)从中随机抽出一张牌,牌面数字是偶数的概率是__________;
(2)先从中随机抽出一张牌,将牌面数字作为十位上的数字(不放回),再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是3的倍数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6![]() ,那么AC=_____.
,那么AC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件8元,出厂价为每件10元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3410元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com