
分析 分别求得两个函数与坐标轴的交点坐标即可求得两函数的图象;分别求得两条直线与x轴的交点坐标后即可求得两条直线在x轴上截的线段的长.
解答 解:令y=0,则x+3=0,解得:x=-3,
将x=0代y=x+3得,y=3,
故y=x+3与x轴交与点(-3,0),与y轴交与点(0,3)
令y=0,则x-2=0,解得:x=-2,
将x=0代y=x-2得,y=-2,
故y=x-2与x轴交与点(2,0),与y轴交与点(0,-2)
故图象为: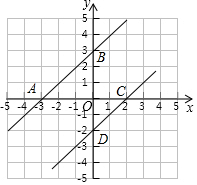
因为直线与y=x+3与x轴交与点(-3,0),直线与y=x-2与x轴交与点(2,0),
所以两条直线与x轴交点间的距离为5.
点评 本题考查了一次函数的图象和一次函数图象上点点坐标特征,解题的关键是利用两点法作出函数的图象.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
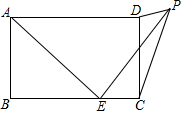 如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长为3或$\frac{5+\sqrt{17}}{2}$.
如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长为3或$\frac{5+\sqrt{17}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com