
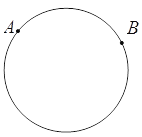
【题目】如图,已知一周长为30cm的圆形轨道上有相距10cm的A、B两点 (备注:圆形轨道上两点的距离是指圆上这两点间较短部分展直后的线段长).动点P从A点出发,以a cm/s的速度,在轨道上按逆时针方向运动,与此同时,动点Q从B出发,以3 cm/s的速度,按同样的方向运动.设运动时间为t (s),当t = 5时,动点P、Q第一次相遇.
(1)求a的值;
(2)若a > 3,在P、Q第二次相遇前,当动点P、Q在轨道上相距12cm时,求t的值.
【答案】(1)a=1或a=7;(2)t的值为0.5、2、8或9.5.
【解析】试题分析:(1)根据相遇时,点P和点Q的运动的路程和等于AB的长列方程即可求解;
(2)设经过ts,P、Q两点相距12cm,分相遇前和相遇后两种情况建立方程求出其解;分点P,Q只能在直线AB上相遇,而点P旋转到直线AB上的时间分两种情况,所以根据题意列出方程分别求解.
试题解析:(1)若a<3,则3×5-5a=10,解得:a=1;
若a>3,则5a-3×5=20,解得:a=7;
(2)∵a>3,∴a=7,共有4种可能:
①7t+10-3t=12,解得:t=0.5;
②7t+10-3t=18,解得:t=2;
③7t+10-3t=42,解得:t=8;
④7t+10-3t=48,解得:t=9.5;
综上所知,t的值为0.5、2、8或9.5.


科目:初中数学 来源: 题型:
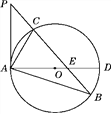
【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 满足
满足![]() ,则称
,则称![]() 互为“相关抛物线”给出如下结论:
互为“相关抛物线”给出如下结论:
①y1与y2的开口方向,开口大小不一定相同; ②y1与y2的对称轴相同;③若y2的最值为m,则y1的最值为k2m;④若函数![]() 与x 轴的两交点间距离为d,则函数
与x 轴的两交点间距离为d,则函数![]() 与x 轴的两交点间距离也为
与x 轴的两交点间距离也为![]() .其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
.其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com