
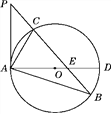
【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)根据圆周角定理得出∠ACD=90°以及利用∠PAC=∠PBA得出∠CAD+∠PAC=90°进而得出答案;
(2)首先得出△CAG∽△BAC,进而得出![]() ,求出AC即可;
,求出AC即可;
(3)先求出AF的长,根据勾股定理得:![]() ,即可得出sin∠ADB=
,即可得出sin∠ADB=![]() ,利用∠ACE=∠ACB=∠ADB,求出即可.
,利用∠ACE=∠ACB=∠ADB,求出即可.
本题解析:(1)证明:连接CD,
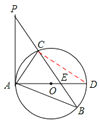
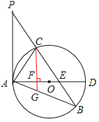
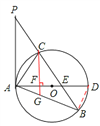
∵AD是⊙O的直径,∴∠ACD=90° ∴∠CAD+∠ADC=90°。
又∵∠PAC=∠PBA,∠ADC=∠PBA, ∴∠PAC=∠ADC。∴∠CAD+∠PAC=90° ∴PA⊥OA。
又∵AD是⊙O的直径,∴PA是⊙O的切线。
(2)由(1)知,PA⊥AD,又∵CF⊥AD,∴CF∥PA。∴∠GCA=∠PAC。
又∵∠PAC=∠PBA,∴∠GCA=∠PBA。
又∵∠CAG=∠BAC,∴△CAG∽△BAC。 ∴![]() ,即AC2=AGAB。
,即AC2=AGAB。
∵AGAB=12,∴AC2=48。∴AC=![]() 。
。
(3)设AF=x, ∵AF:FD=1:2,∴FD=2x。∴AD=AF+FD=3x。
在Rt△ACD中,∵CF⊥AD,∴AC2=AFAD,即3x2=48。
解得;x=4。 ∴AF=4,AD=12。∴⊙O半径为6。
在Rt△AFG中,∵AF=4,GF=2,
∴根据勾股定理得:![]()
由(2)知,AGAB=48 ![]()
连接BD,∵AD是⊙O的直径,∴∠ABD=90°。
在Rt△ABD中,∵sin∠ADB=![]() ,AD=12,
,AD=12,![]() ∴sin∠ADB=
∴sin∠ADB=![]() 。
。
∵∠ACE=∠ACB=∠ADB,∴sin∠ACE=![]() .
.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 某学习小组经过合作交流,给出了下面的解题思路:
(1)请你按照他们的解题思路过程完成解答过程;
(2)填空:在△DEF中,DE=15,EF=13,DF=4,则△DEF的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
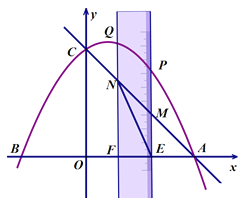
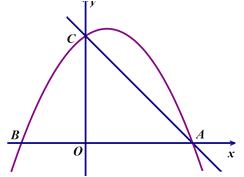
【题目】如图,已知抛物线![]() 与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
(1)求点A、B、C的坐标;
(2)当点M和点N都在线段AC上时,连接EN,如果点E的坐标为(4,0),求sin∠ANE的值;
(3)在刻度尺平移过程中,当以点P、Q、N、M为顶点的四边形是平行四边形时,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车同时分别从A、B两城沿同一条高速公路驶向C城.已知A、C两城的距离为450千米,B、C两城的距离为400千米,甲车比乙车的速度快10千米/时,结果两辆车同时到达C城.求两车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,如![]() 表示5、3在数轴上对应的两点之间的距离;
表示5、3在数轴上对应的两点之间的距离; ![]() ,所以
,所以![]() 表示5、﹣3在数轴上对应的两点之间的距离;
表示5、﹣3在数轴上对应的两点之间的距离; ![]() ,所以
,所以![]() 表示5在数轴上对应的点到原点的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为
表示5在数轴上对应的点到原点的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为![]() .
.
问题(1):点A、B、C在数轴上分别表示有理数x、﹣2、1,那么A到B的距离与A到C的距离之和可表示为 (用含绝对值的式子表示).
问题(2):利用数轴探究:
①找出满足![]() 的x的所有值是 ,
的x的所有值是 ,
②设![]() ,当x的值取在不小于﹣1且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是 ;当x的取值范围是 时,
,当x的值取在不小于﹣1且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是 ;当x的取值范围是 时, ![]() 取得最小值,最小值是 .
取得最小值,最小值是 .
问题(3):求![]() 的最小值以及此时x的值;
的最小值以及此时x的值;
问题(4): ![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
某管道由甲、乙两工程队单独施工分别需要30天、20天.
(1)如果两队从管道两端同时施工,需要多少天完工?
(2)又知甲队单独施工每天需付200元施工费,乙队单独施工每天需付280元施工费,那么是由甲队单独施工,还是由乙队单独施工,还是由两队同时施工?请你按照少花钱多办事的原则,设计一个方案,并通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
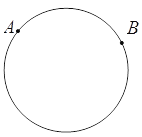
【题目】如图,已知一周长为30cm的圆形轨道上有相距10cm的A、B两点 (备注:圆形轨道上两点的距离是指圆上这两点间较短部分展直后的线段长).动点P从A点出发,以a cm/s的速度,在轨道上按逆时针方向运动,与此同时,动点Q从B出发,以3 cm/s的速度,按同样的方向运动.设运动时间为t (s),当t = 5时,动点P、Q第一次相遇.
(1)求a的值;
(2)若a > 3,在P、Q第二次相遇前,当动点P、Q在轨道上相距12cm时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com