
【题目】(10分)如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
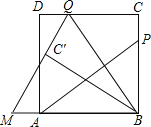
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
【答案】(1)AP=BQ,理由参见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)利用BQ⊥AP和四边形ABCD是正方形的条件证明△PBA≌△QCB即可;(2)过点Q作QH⊥AB于H,可得QH=BC=AB=3,∵BP=2PC,∴BP=2,PC=1,运用勾股定理可求得AP(即BQ)=![]() ,BH=2.由DC∥AB,得∠CQB=∠QBA.由折叠角相等可得∠C′QB=∠CQB,等量代换:∠QBA=∠C′QB,根据等角对等边得:MQ=MB.设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中运用勾股定理求得QM;(3)过点Q作QH⊥AB于H,用(2)的思路方法求出QM的长,也就知道BM的长了,再减去AB的长就是AM的长.
,BH=2.由DC∥AB,得∠CQB=∠QBA.由折叠角相等可得∠C′QB=∠CQB,等量代换:∠QBA=∠C′QB,根据等角对等边得:MQ=MB.设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中运用勾股定理求得QM;(3)过点Q作QH⊥AB于H,用(2)的思路方法求出QM的长,也就知道BM的长了,再减去AB的长就是AM的长.
试题解析:(1)证明线段相等,通常证明所在的三角形全等,此题利用BQ⊥AP和四边形ABCD是正方形的条件证明△PBA≌△QCB,证明:∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠C=90°,∴∠ABQ+∠CBQ=90°.∵BQ⊥AP,∴∠PAB+∠QBA=90°,∴∠PAB=∠CBQ(同角的余角相等).∴△PBA≌△QCB(ASA),∴AP=BQ(全等三角形的对应边相等);(2)过点Q作QH⊥AB于H,如图:∵四边形ABCD是正方形,∴QH=BC=AB=3.∵BP=2PC,BP+PC=3,∴BP=2,PC=1,∵△PBA≌△QCB,∴CQ=BP=2,四边形QHCB是矩形,∴BH=CQ=2,∵四边形ABCD是正方形,∴DC∥AB,∴∠CQB=∠QBA.由折叠角相等可得∠C′QB=∠CQB,∴∠QBA=∠C′QB(等量代换),∴MQ=MB(等角对等边).设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中,根据勾股定理可得x2=(x﹣2)2+32,解得x=![]() .∴QM的长为
.∴QM的长为![]() ;
;
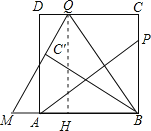
过点Q作QH⊥AB于H,如上题的思路可得:四边形ABCD是正方形,BP=m,PC=n,∴QH=BC=AB=m+n.∵△PBA≌△QCB,∴CQ=BP=m,四边形QHCB是矩形,∴BH=CQ=m.设QM=x,则有MB=QM=x,MH=x﹣m.在Rt△MHQ中,根据勾股定理可得x2=(x﹣m)2+(m+n)2,解得x=m+n+![]() ,∴AM=MB﹣AB=m+n+
,∴AM=MB﹣AB=m+n+![]() ﹣m﹣n=
﹣m﹣n=![]() .即AM的长为
.即AM的长为![]() .
.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份 | 4月 | 5月 | 6月 |
用水量 | 15 | 17 | 21 |
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=_______,△APE的面积等于8.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)13+(﹣15)﹣(﹣23);
(2)23×(﹣5)﹣(﹣3)÷![]() ;
;
(3)﹣14﹣![]() ×[2﹣(﹣3)2];
×[2﹣(﹣3)2];
(4)﹣(2y﹣5)+(4+3y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=2,正确的个数为( ) 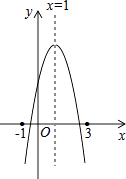
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线y= ![]() 的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( )
的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( ) 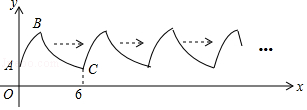
A.72
B.36
C.16
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的手机没电了,现有一个只含A,B,C,D四个同型号插座的插线板(如图,假设每个插座都适合所有的充电插头,且被选中的可能性相同),请计算: 
(1)若小明随机选择一个插座插入,则插入A的概率为;
(2)现小明对手机和学习机两种电器充电,请用列表或画树状图的方法表示出两个插头插入插座的所有可能情况,并计算两个插头插在相邻插座的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com