
【题目】某校为了解2014年八年级学生课外书籍借阅情况,从中随机抽取了50名学生课外书籍借阅情况,将统计结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这50名学生借阅总册数的40%.
类别 | 科普类 | 教辅类 | 文艺类 | 其他 |
册数(本) | 168 | 105 | m | 32 |
(1)表格中字母m的值等于 ;
(2)扇形统计图中“教辅类”所对应的圆心角α的度数为 °;
(3)该校2014年八年级有600名学生,请你估计该年级学生共借阅教辅类书籍约多少本?

【答案】(1)115;(2)90;(3)1260.
【解析】
(1)首先根据科普类所占的百分比和册数求得总册数,然后相减即可求得m的值;
(2)用教辅类书籍除以总册数乘以周角即可求得其圆心角的度数;
(3)用该年级的总人数乘以教辅类的学生所占比例,即可求出该年级共借阅教辅类书籍人数.
(1)观察扇形统计图知:科普类有168册,占40%,
∴借阅总册数为168÷40%=420本,
∴m=420-168-105-32=115;
(2)教辅类的圆心角为:360°×![]() =90°;
=90°;
(3)设全校600名学生借阅教辅类书籍为x本,
根据题意得:![]() ,
,
解得:x=1260,
所以该年级学生共借阅教辅类书籍约1260本.


科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应的任务;全等四边形根据全等图形的定又可知:四条边分别相等、四个角也分别相等的两个四边形全等。在“探索三角形全等的条件”时,我们把两个三角形中“一条边和等”或“一个角相等”称为一个条件.智慧小组的同学类比“探索三角形全等条件”的方法探索“四边形全等的条件”,进行了如下思考:如图1,四边形![]() 和四边形
和四边形![]() 中,连接对角线
中,连接对角线![]() ,这样两个四边形全等的问题就转化为“
,这样两个四边形全等的问题就转化为“![]() ”与“
”与“![]() ”的问题。若先给定“
”的问题。若先给定“![]() ”的条件,只要再增加
”的条件,只要再增加![]() 个条件使“
个条件使“![]() ”即可推出两个四边形中“四条边分别相等、四个角也分别和等”,从而说明两个四边形全等。
”即可推出两个四边形中“四条边分别相等、四个角也分别和等”,从而说明两个四边形全等。
按照智慧小组的思路,小明对图![]() 中的四边形
中的四边形![]() 与四边形
与四边形![]() 先给出和下条件:
先给出和下条件: ![]() ,
,![]() ,小亮在此基础上又给出“
,小亮在此基础上又给出“![]() ”两个条件.他们认为满足这五个条件能得到“四边形
”两个条件.他们认为满足这五个条件能得到“四边形![]() 四边形
四边形![]() ”.
”.

(1)请根据小明和小亮给出的条件,说明“四边形![]() 四边形
四边形![]() ”的理由;
”的理由;
(2)请从下面![]() 两题中任选一题作答,我选择 题.
两题中任选一题作答,我选择 题.
![]() 在材料中“小明所给条件”的基础上,小颖又给出两个条件“
在材料中“小明所给条件”的基础上,小颖又给出两个条件“![]() ”.满足这五个条件 (填“能”或“不能”)得到四边形
”.满足这五个条件 (填“能”或“不能”)得到四边形![]() 四边形
四边形![]()
![]() 在材料中“小明所给条件的基础上”,再添加两个关于原四边形的条件(要求:不同于小亮的条件),使四边形
在材料中“小明所给条件的基础上”,再添加两个关于原四边形的条件(要求:不同于小亮的条件),使四边形![]() 四边形
四边形![]() ,你添加的条件是① ,② .
,你添加的条件是① ,② .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() △ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
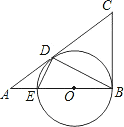
(1)求证:BC=CD;
(2)求证:∠ADE=∠ABD;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为160元,200元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入/元 | |
A种型号/台 | B种型号/台 | ||
第1周 | 3 | 5 | 1800 |
第2周 | 4 | 10 | 3200 |
(1)A、B两种型号的电风扇的销售单价是多少?
(2)若该超市准备用不多于5400元的金额再次采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠ABC=60°,M为AD中点,P为对角线BD上一动点,连接PA和PM,则PA+PM的最小值是( )

A.3B.2![]() C.3
C.3![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】影响刹车距离的最主要因素是汽车行驶的速度及路面的摩擦系数.有研究表明,晴天在某段公路上行驶时,速度v(km/h)的汽车的刹车距离s(m)可以由公式![]() 确定;雨天行驶时,这一公式为
确定;雨天行驶时,这一公式为![]() .
.
(1)如果行车速度是70 km/h,那么在雨天行驶和在晴天行驶相比,刹车距离相差多少米?
(2)如果行车速度分别是60 km/h与80 km/h,那么同在雨天行驶(相同的路面)相比,刹车距离相差多少?
(3)根据上述两点分析,你想对司机师傅说些什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形△ABC中,D是BC边的中点,AD=![]() BC.
BC.
(1)△ABC的形状为 .
(2)如图,BM=3,BC=12,∠B=45°,∠MAN=45°,求CN;
(3)在(2)的条件下,AN= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现)任意三个连续偶数的平方和是4的倍数。
(验证)(1)![]() 的结果是4的几倍?
的结果是4的几倍?
(2)设三个连续偶数的中间一个为![]() ,写出它们的平方和,并说明是4的倍数。
,写出它们的平方和,并说明是4的倍数。
(延伸)(3)设三个连续奇数的中间一个数为![]() ,写出它们的平方和,它是12的倍数吗?若是,说明理由,若不是,写出被12除余数是多少?
,写出它们的平方和,它是12的倍数吗?若是,说明理由,若不是,写出被12除余数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com