
【题目】如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度( ![]() =1.7).
=1.7). 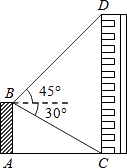
【答案】解:如图,过点B作BE⊥CD于点E,
根据题意,∠DBE=45°,∠CBE=30°.
∵AB⊥AC,CD⊥AC,
∴四边形ABEC为矩形.
∴CE=AB=12m.
在Rt△CBE中,cot∠CBE= ![]() ,
,
∴BE=CEcot30°=12× ![]() =12
=12 ![]() .
.
在Rt△BDE中,由∠DBE=45°,
得DE=BE=12 ![]() .
.
∴CD=CE+DE=12( ![]() +1)≈32.4.
+1)≈32.4.
答:楼房CD的高度约为32.4m.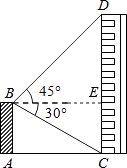
【解析】首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造关系式求解.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】已知实数a,b,c满足(a-![]() )2+
)2+![]() +|c-2
+|c-2![]() |=0.
|=0.
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能构成三角形,求出三角形的周长和面积;若不能构成三角形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc﹣ad.
例如:(1,2)★(3,4)=2×3﹣1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,﹣3)★(3,﹣2)= ;
(2)若有理数对(﹣3,2x﹣1)★(1,x+1)=7,则x= ;
(3)当满足等式(﹣3,2x﹣1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件画图
如图示点A、B、C分别代表三个村庄.
(1)画射线AC;
(2)画线段AB;
(3)若线段AB是连结A村和B村的一条公路,现C村庄也要修一条公路与A、B两村庄之间的公路连通,为了减少修路开支,C村庄应该如何修路?请在同一图上用三角板画出示意图,并说明画图理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E、F分别是AB、CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE、BF交于点M、N.求证:△ABN≌△CDM.

查看答案和解析>>
科目:初中数学 来源: 题型:
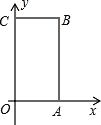
【题目】如图,长方形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(6,0),(0,10),点B在第一象限内.
(1)写出点B的坐标,并求长方形OABC的周长;
(2)若有过点C的直线CD把长方形OABC的周长分成3:5两部分,D为直线CD与长方形的边的交点,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
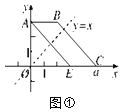
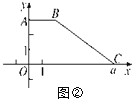
【题目】如图①,在平面直角坐标系xOy中,已知点A(0,3),B(2,3),OC=a.将梯形ABCO沿直线y=x折叠,点A落在线段OC上,对应点为E.
(1)求点E的坐标;
(2)①若BC∥AE,求a的值;(提示:两边互相平行的四边形是平行四边形,平行四边形的对边相等)
②如图②,若梯形ABCO的面积为2a,且直线y=mx将此梯形面积分为1∶2的两部分,求直线y=mx的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个口袋中装有七个完全相同的小球,小球上分别标有-3、-2、-1、0、1、2、3七个数,搅匀后一次从中摸出一个小球,将小球上的数用![]() 表示,将
表示,将![]() 的值分别代入函数
的值分别代入函数![]() 和方程
和方程![]() ,恰好使得函数的图像经过二、四象限,且方程有整数解,那么这7个数中所有满足条件的
,恰好使得函数的图像经过二、四象限,且方程有整数解,那么这7个数中所有满足条件的![]() 的值之和是( )
的值之和是( )
A. 1 B. -1 C. -3 D. -4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com