
【题目】大豆是一种非常受欢迎的农作物,已知种植某种大豆的平均产量为![]() 吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价
吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价![]() 千元/吨与种植大豆的面积
千元/吨与种植大豆的面积![]() 公顷之间关系如图所示:
公顷之间关系如图所示:
为了鼓励农民种植粮食的热情,市政府出台相关政策:对本市种植大豆的农民按保护价4.5千元/吨进行补偿(即当销售单价低于4.5千元/吨时,差价由政府提供补助,比如销售单价为4千元/吨,则政府补贴农民0.5千元/吨,若单价不少于4.5千元/吨时,则不补助)。
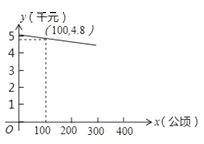
(1)若该市计划种植大豆300公顷,销售后是否享受政府补贴?若享受则享受补贴总金额是多少千元?
(2)设该市销售大豆获得的利润(不含政府补贴部分)为w千元,当种植面积为多少公顷时利润最大,最大利润是多少千元?注:销售利润=(销售单价×每公顷产量-每公顷成本)×公顷数
(3)为保证所得的总利润(含可能得到的政府补贴)达到748千元,应该种植多少公顷大豆?
【答案】(1)享受补贴,总金额75千元;(2)450公顷时利润最大,最大为1012.5千元;(3)220公顷大豆
【解析】
(1)利用待定系数法求得销售大豆的单价y千元/吨与种植大豆的面积x公顷之间关系式,再代入x=300,求得y,进一步判定计算即可;
(2)利用销售利润=(销售单价×每公顷产量-每公顷成本)×公顷数列出函数解析式,利用配方法解答即可;
(3)利用(2)中求得的函数解析式,分享受政府补贴和不享受补贴两种情况与748建立方程求得答案并检验即可.
解:(1)设销售大豆的单价y千元/吨与种植大豆的面积x公顷之间关系式为y=kx+5,
代入(100,4.8)得k=![]() ,则
,则![]() ,
,
当x=300时, ![]() ,
,
∴享受补贴,补贴总金额是:(4.54.4)×300×2.5=75(千元).
答:销售后享受政府补贴,则补贴总金额是75千元.
(2)由题意得![]() ,
,
即当x=450时,W取得最大值,也就是当种植面积为450公顷时,利润最大,最大利润是1012.5千元.
(3)令![]() 得
得![]()
∴当![]() 时,不享受补贴,
时,不享受补贴,
令![]() ,解得
,解得![]() ,
,
当![]() 时,令
时,令![]() ,解得
,解得![]() ,不成立,
,不成立,
综上所述:应种植220公顷大豆.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
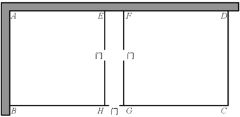
【题目】某农场要建一个饲养场(矩形ABCD)两面靠现有墙(AD位置的墙最大可用长度为27米,AB位置的墙最大可用长度为15米),另两边用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图所示的三处各留1米宽的门(不用木栏)。建成后木栏总长45米。设饲养场(矩形ABCD)的一边AB长为x米.
(1)饲养场另一边BC= 米(用含x的代数式表示).
(2)若饲养场的面积为180平方米,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“两个黄鹂鸣翠柳”.
(1)小明回答该问题时,对第二个字是选“个”还是选“只”难以抉择,若随机选择其中一个,则小明回答正确的概率是__________;
(2)小丽回答该问题时,对第二个字是选“个”还是选“只”、第五个字是选“鸣”还是选“明”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
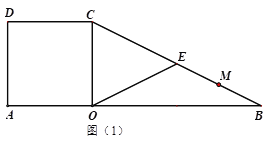
【题目】如图(1),在边长为4的正方形![]() 中,在AO的延长线上取点B,使OB=2OA,连接BC.
中,在AO的延长线上取点B,使OB=2OA,连接BC.
(1)点![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() ,求线段
,求线段![]() 的长;
的长;
(2)点M在线段BC上,且到OB,OC的距离分别为![]() ,
,![]() ,当
,当![]() 时, 求
时, 求![]() ,
,![]() 的值;
的值;
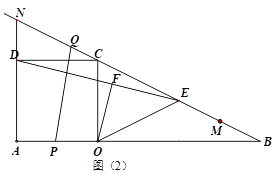
(3)如图(2),在第(1)、(2)问条件下,延长![]() 交直线
交直线![]() 于点N,动点
于点N,动点![]() 在
在![]() 上从点
上从点![]() 向终点
向终点![]() 匀速运动,同时,动点
匀速运动,同时,动点![]() 在
在![]() 延长线上,沿直线
延长线上,沿直线![]() 向终点M匀速运动,它们同时出发且同时到达终点.当点
向终点M匀速运动,它们同时出发且同时到达终点.当点![]() 运动到
运动到![]() 中点时,点
中点时,点![]() 恰好与点
恰好与点![]() 重合.
重合.
①在运动过程中,设点![]() 的运动路程为s,
的运动路程为s,![]() ,用含t的代数式表示s.
,用含t的代数式表示s.
②过点O作![]() 于点
于点![]() ,在运动路程中,当
,在运动路程中,当![]() 与
与![]() 的一边平行时,求所有满足条件的
的一边平行时,求所有满足条件的![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中的每个小正方形的边长是1,每个小正方形的顶点叫做格点。已知,![]() 的顶点都在格点上,
的顶点都在格点上,![]() ,
,![]() ,若在边上
,若在边上![]() 上以某个格点
上以某个格点![]() 为端点画出长是
为端点画出长是![]() 的线段
的线段![]() ,使线段另一端点
,使线段另一端点![]() 恰好落在边
恰好落在边![]() 上,且线段
上,且线段![]() 与点
与点![]() 构成的三角形与
构成的三角形与![]() 相似,请你在两个图中画出线段
相似,请你在两个图中画出线段![]() (不必说明理由)。
(不必说明理由)。
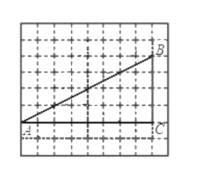
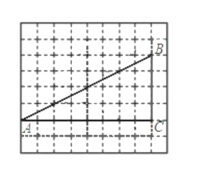
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一位篮球运动员在距离篮圈中心水平距离![]() 处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为
处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为![]() 时,达到最大高度
时,达到最大高度![]() ,然后准确落入篮筐内,已知篮圈中心距离地面高度为
,然后准确落入篮筐内,已知篮圈中心距离地面高度为![]() ,试解答下列问题:
,试解答下列问题:
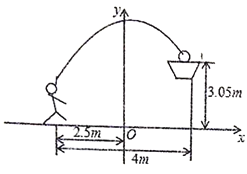
(1)建立图中所示的平面直角坐标系,求抛物线所对应的函数表达式.
(2)这次跳投时,球出手处离地面多高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线顶点为A(1,2),且过原点,与x轴的另一个交点为B,
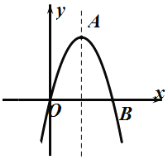
(1)求抛物线的解析式和B点坐标;
(2)抛物线上是否存在点M,使△OBM的面积等于2?若存在,请写出M点坐标,若不存在,说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连结EC.如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图1,请你判断线段CE、BD之间的位置和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2画出图形,判断①中的结论是否仍然成立,并证明你的判断.

查看答案和解析>>
科目:初中数学 来源: 题型:
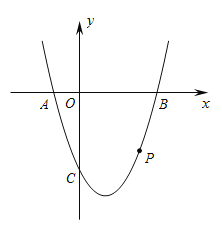
【题目】如图,抛物线![]() 与x轴相交于
与x轴相交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() .
.![]() 为抛物线上一点,横坐标为
为抛物线上一点,横坐标为![]() ,且
,且![]() .
.
⑴求此抛物线的解析式;
⑵当点![]() 位于
位于![]() 轴下方时,求
轴下方时,求![]() 面积的最大值;
面积的最大值;
⑶设此抛物线在点![]() 与点
与点![]() 之间部分(含点
之间部分(含点![]() 和点
和点![]() )最高点与最低点的纵坐标之差为
)最高点与最低点的纵坐标之差为![]() .
.
①求![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 时,直接写出
时,直接写出![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com