
【题目】如图,网格中的每个小正方形的边长是1,每个小正方形的顶点叫做格点。已知,![]() 的顶点都在格点上,
的顶点都在格点上,![]() ,
,![]() ,若在边上
,若在边上![]() 上以某个格点
上以某个格点![]() 为端点画出长是
为端点画出长是![]() 的线段
的线段![]() ,使线段另一端点
,使线段另一端点![]() 恰好落在边
恰好落在边![]() 上,且线段
上,且线段![]() 与点
与点![]() 构成的三角形与
构成的三角形与![]() 相似,请你在两个图中画出线段
相似,请你在两个图中画出线段![]() (不必说明理由)。
(不必说明理由)。
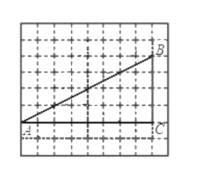
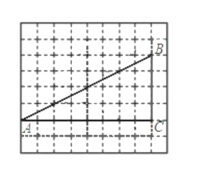
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx﹣3与x轴交于A点,与y轴交于C点,且A(1,0)、B(3,0),点D是抛物线的顶点.
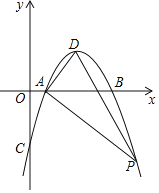
(1)求抛物线的解析式
(2)在y轴上是否存在M点,使得△MAC是以AC为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
(3)点P为抛物线上的动点,且在对称轴右侧,若△ADP面积为3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
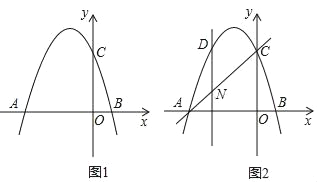
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
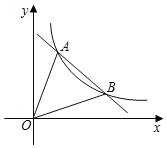
【题目】如图所示,双曲线y=![]() (x>0,k>0)与直线y=ax+b(a≠0,b为常数)交于A(2,4),B(m,2)两点.
(x>0,k>0)与直线y=ax+b(a≠0,b为常数)交于A(2,4),B(m,2)两点.
(1)求m的值;
(2)若C点坐标为(n,0),当AC+BC的值最小时,求出n的值;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
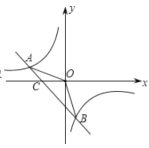
【题目】如图,已知![]() ,
,![]() 是一次函数
是一次函数![]() 和反比例函数
和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求![]() 的面积;
的面积;
(3)根据图象直接写出![]() 的
的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
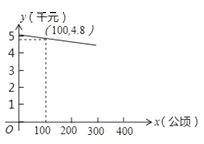
【题目】大豆是一种非常受欢迎的农作物,已知种植某种大豆的平均产量为![]() 吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价
吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价![]() 千元/吨与种植大豆的面积
千元/吨与种植大豆的面积![]() 公顷之间关系如图所示:
公顷之间关系如图所示:
为了鼓励农民种植粮食的热情,市政府出台相关政策:对本市种植大豆的农民按保护价4.5千元/吨进行补偿(即当销售单价低于4.5千元/吨时,差价由政府提供补助,比如销售单价为4千元/吨,则政府补贴农民0.5千元/吨,若单价不少于4.5千元/吨时,则不补助)。
(1)若该市计划种植大豆300公顷,销售后是否享受政府补贴?若享受则享受补贴总金额是多少千元?
(2)设该市销售大豆获得的利润(不含政府补贴部分)为w千元,当种植面积为多少公顷时利润最大,最大利润是多少千元?注:销售利润=(销售单价×每公顷产量-每公顷成本)×公顷数
(3)为保证所得的总利润(含可能得到的政府补贴)达到748千元,应该种植多少公顷大豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
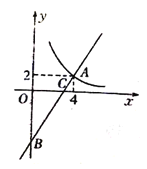
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,且
,且![]() .
.
(1)求函数![]() 和
和![]() 的表达式.
的表达式.
(2)已知直线![]() 与
与![]() 轴相交于点
轴相交于点![]() 在第一象限内,求反比例函数
在第一象限内,求反比例函数![]() 的图象上一点
的图象上一点![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记
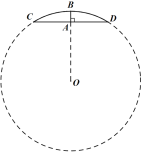
载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①)
阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊥CD于点A,求间径就是要求⊙O的直径.再次阅读后,发现AB=______寸,CD=____寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件,并帮助小智求出⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一个直角墙角修建一个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD总长为12m,则该梯形储料场ABCD的最大面积是( )

A.18m2B.![]() m2C.
m2C.![]() m2D.
m2D.![]() m2
m2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com