
【题目】如图所示,双曲线y=![]() (x>0,k>0)与直线y=ax+b(a≠0,b为常数)交于A(2,4),B(m,2)两点.
(x>0,k>0)与直线y=ax+b(a≠0,b为常数)交于A(2,4),B(m,2)两点.
(1)求m的值;
(2)若C点坐标为(n,0),当AC+BC的值最小时,求出n的值;
(3)求△AOB的面积.
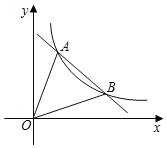
【答案】(1)m=4;(2)n=![]() ;(3)6.
;(3)6.
【解析】
(1)由A点坐标即可求出反比例函数,再把B点坐标代入反比函数即可求出m的值;
(2)求得B点关于x轴的对称点B′(4,-2),连接AB′,交x轴与C,此时AC+BC=AB′,AC+BC的值最小,根据待定系数法求得直线AB′的解析式,然后把(n,0)代入求得的解析式即可求得n的值;
(3)根据待定系数法求得直线AB的解析式,即可得到直线AB与x轴的交点C的坐标,然后根据S△AOB=S△AOC-S△BOC求得即可.
解:(1)把A(2,4)代入y=![]() (x>0,k>0),
(x>0,k>0),
∴k=2×4=8,
∴反比例函数的解析式为y=![]() ,
,
把B(m,2)代入y=![]() 得,2=
得,2=![]() ,
,
解得m=4;
(2)由(1)可知:A(2,4),B(4,2),
∴B点关于x轴的对称点B′(4,﹣2),
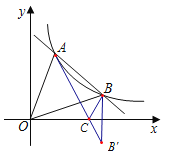
连接AB′,交x轴与C,此时AC+BC=AB′,AC+BC的值最小,
设直线AB′的解析式为y=ax+b,
把A(2,4),B′(4,﹣2)代入得![]() ,
,
解得:![]() ,
,
∴直线AB′的解析式为y=﹣3x+10,
把(n,0)代入得y=﹣3n+10,
∴n=![]() ;
;
(3)设直线AB的解析式为y=mx+t,
∴把A(2,4),B(4,2)代入得![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣x+6,
∴直线AB与x轴的交点C(6,0),
∴S△AOB=S△AOC﹣S△BOC=![]() ×6×4﹣
×6×4﹣![]() ×6×2=6.
×6×2=6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线![]() 经过B,C两点,点A是抛物线与x轴的另一个交点.
经过B,C两点,点A是抛物线与x轴的另一个交点.

(1)求出点B和点C的坐标.
(2)求此抛物线的函数解析式.
(3)在抛物线x轴上方存在一点P(不与点C重合),使![]() ,请求出点P的坐标.
,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.
(1)摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为________.
(2)摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“两个黄鹂鸣翠柳”.
(1)小明回答该问题时,对第二个字是选“个”还是选“只”难以抉择,若随机选择其中一个,则小明回答正确的概率是__________;
(2)小丽回答该问题时,对第二个字是选“个”还是选“只”、第五个字是选“鸣”还是选“明”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
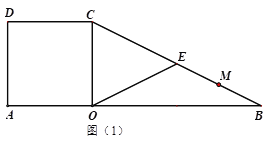
【题目】如图(1),在边长为4的正方形![]() 中,在AO的延长线上取点B,使OB=2OA,连接BC.
中,在AO的延长线上取点B,使OB=2OA,连接BC.
(1)点![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() ,求线段
,求线段![]() 的长;
的长;
(2)点M在线段BC上,且到OB,OC的距离分别为![]() ,
,![]() ,当
,当![]() 时, 求
时, 求![]() ,
,![]() 的值;
的值;
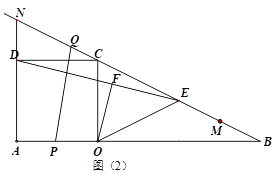
(3)如图(2),在第(1)、(2)问条件下,延长![]() 交直线
交直线![]() 于点N,动点
于点N,动点![]() 在
在![]() 上从点
上从点![]() 向终点
向终点![]() 匀速运动,同时,动点
匀速运动,同时,动点![]() 在
在![]() 延长线上,沿直线
延长线上,沿直线![]() 向终点M匀速运动,它们同时出发且同时到达终点.当点
向终点M匀速运动,它们同时出发且同时到达终点.当点![]() 运动到
运动到![]() 中点时,点
中点时,点![]() 恰好与点
恰好与点![]() 重合.
重合.
①在运动过程中,设点![]() 的运动路程为s,
的运动路程为s,![]() ,用含t的代数式表示s.
,用含t的代数式表示s.
②过点O作![]() 于点
于点![]() ,在运动路程中,当
,在运动路程中,当![]() 与
与![]() 的一边平行时,求所有满足条件的
的一边平行时,求所有满足条件的![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
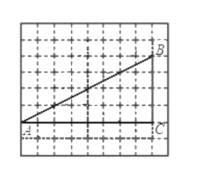
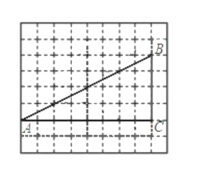
【题目】如图,网格中的每个小正方形的边长是1,每个小正方形的顶点叫做格点。已知,![]() 的顶点都在格点上,
的顶点都在格点上,![]() ,
,![]() ,若在边上
,若在边上![]() 上以某个格点
上以某个格点![]() 为端点画出长是
为端点画出长是![]() 的线段
的线段![]() ,使线段另一端点
,使线段另一端点![]() 恰好落在边
恰好落在边![]() 上,且线段
上,且线段![]() 与点
与点![]() 构成的三角形与
构成的三角形与![]() 相似,请你在两个图中画出线段
相似,请你在两个图中画出线段![]() (不必说明理由)。
(不必说明理由)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线顶点为A(1,2),且过原点,与x轴的另一个交点为B,
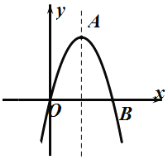
(1)求抛物线的解析式和B点坐标;
(2)抛物线上是否存在点M,使△OBM的面积等于2?若存在,请写出M点坐标,若不存在,说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的高.
边上的高.
问题发现:
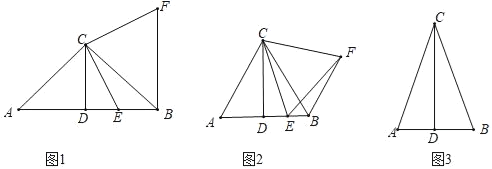
(1)如图1,若![]() ,点
,点![]() 是线段
是线段![]() 上一个动点(点
上一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合)连接
重合)连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() ,我们会发现
,我们会发现![]() 、
、![]() 、
、![]() 之间的数量关系是
之间的数量关系是![]() ,请你证明这个结论;
,请你证明这个结论;
提出猜想:
(2)如图2,若![]() ,点
,点![]() 是线段
是线段![]() 上一个动点(点
上一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合)连接
重合)连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() ,猜想线段
,猜想线段![]() 、
、![]() 、
、![]() 之间的数量关系是_______;
之间的数量关系是_______;
拓广探索:
(3)若![]() ,
,![]() (
(![]() 为常数),点
为常数),点![]() 是线段
是线段![]() 上一个动点(点
上一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() .请你利用上述条件,根据前面的解答过程得出类似的猜想,并在图3中画出图形,标明字母,不必解答.
.请你利用上述条件,根据前面的解答过程得出类似的猜想,并在图3中画出图形,标明字母,不必解答.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com