
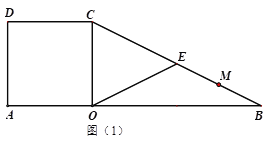
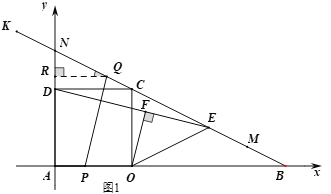
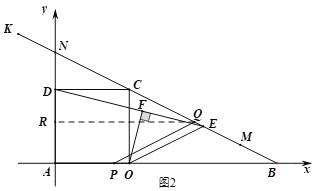
����Ŀ����ͼ��1�����ڱ߳�Ϊ4��������![]() �У���AO���ӳ�����ȡ��B��ʹOB=2OA������BC��
�У���AO���ӳ�����ȡ��B��ʹOB=2OA������BC��
��1����![]() ���߶�
���߶�![]() ���е㣬����
���е㣬����![]() �����߶�
�����߶�![]() �ij���
�ij���
��2����M���߶�BC�ϣ��ҵ�OB��OC�ľ���ֱ�Ϊ![]() ��
��![]() ����
����![]() ʱ�� ��
ʱ�� ��![]() ��
��![]() ��ֵ��
��ֵ��
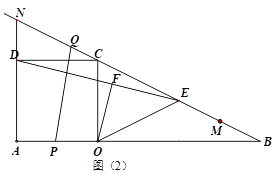
��3����ͼ��2�����ڵڣ�1������2���������£��ӳ�![]() ��ֱ��
��ֱ��![]() �ڵ�N������
�ڵ�N������![]() ��
��![]() �ϴӵ�
�ϴӵ�![]() ���յ�
���յ�![]() �����˶���ͬʱ������
�����˶���ͬʱ������![]() ��
��![]() �ӳ����ϣ���ֱ��
�ӳ����ϣ���ֱ��![]() ���յ�M�����˶�������ͬʱ������ͬʱ�����յ㣮����
���յ�M�����˶�������ͬʱ������ͬʱ�����յ㣮����![]() �˶���
�˶���![]() �е�ʱ����
�е�ʱ����![]() ǡ�����
ǡ�����![]() �غϣ�
�غϣ�
�����˶������У����![]() ���˶�·��Ϊs��
���˶�·��Ϊs��![]() ���ú�t�Ĵ���ʽ��ʾs��
���ú�t�Ĵ���ʽ��ʾs��
�ڹ���O��![]() �ڵ�
�ڵ�![]() �����˶�·���У���
�����˶�·���У���![]() ��
��![]() ��һ��ƽ��ʱ������������������
��һ��ƽ��ʱ������������������![]() �ij���
�ij���
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3����
����3����![]() ����
����![]() ��
��![]() .
.
��������
��1���ȸ��ݹ��ɶ������BC�ij���������ֱ�������ε����ʼ�����ý����
��2������M��MG��OB��MH��OC������֤��BMG�ס�BCO���������������ε����ʲ������֪![]() �������m��n��ֵ��
�������m��n��ֵ��
��3����������֪������![]() �˶���
�˶���![]() �е�ʱ����
�е�ʱ����![]() ǡ�����
ǡ�����![]() �غϣ����Ե���
�غϣ����Ե���![]() ��
��![]() �е��˶�����Oʱ����
�е��˶�����Oʱ����![]() ǡ����ӵ�
ǡ����ӵ�![]() �˶�����M���ݴ��г�����ʽ���ɵó�s��t�Ĺ�ϵʽ��
�˶�����M���ݴ��г�����ʽ���ɵó�s��t�Ĺ�ϵʽ��
����ȷ����Q�ij�����K��λ�ã����������![]() ���ٽ�����ͼ1��ʾ��ƽ��ֱ������ϵ����Ȼ�ڵ�P���˶������У�PQ��DEʼ�ղ�ƽ�У���PQ��OFʱ����������ϵ������ֱ�ߴ�ֱʱ����
���ٽ�����ͼ1��ʾ��ƽ��ֱ������ϵ����Ȼ�ڵ�P���˶������У�PQ��DEʼ�ղ�ƽ�У���PQ��OFʱ����������ϵ������ֱ�ߴ�ֱʱ����![]() ��������ú�t�IJ�����ʾ��ֱ��PQ�Ľ���ʽ������ֱ��BC�����������������Q�����꣬Ȼ������������Ǻ�����֪ʶ���QNֵ������QK�ij��������âٵĽ��ۼ��ù���t�ķ��̣��ⷽ�̼������t��ֵ����PQ��OEʱ����ͼ2����������ϵ����ֱ��ƽ��
��������ú�t�IJ�����ʾ��ֱ��PQ�Ľ���ʽ������ֱ��BC�����������������Q�����꣬Ȼ������������Ǻ�����֪ʶ���QNֵ������QK�ij��������âٵĽ��ۼ��ù���t�ķ��̣��ⷽ�̼������t��ֵ����PQ��OEʱ����ͼ2����������ϵ����ֱ��ƽ��![]() ��ͬ�����˼·��⼴��.
��ͬ�����˼·��⼴��.
�⣺��1�����ı���![]() �������Σ���OC=AO=4����COA=90�������COB=90����
����������OC=AO=4����COA=90�������COB=90����
��OB=2OA����OB=8����![]() ��
��
�ߵ�![]() ���߶�
���߶�![]() ���е㣬��
���е㣬��![]() ��
��
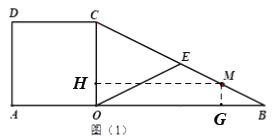
��2����ͼ��1��������M��MG��OB��MH��OC����MG=m��MH=n=OG��MG��OC��
���BMG�ס�BCO����![]() ����
����![]() ��
��
��![]() ����n=6mʱ��
����n=6mʱ��![]() ����ã�m=1����n=6��
����ã�m=1����n=6��
��![]() ��
��![]() ��
��
��3����������֪������![]() �˶���
�˶���![]() �е�ʱ����
�е�ʱ����![]() ǡ�����
ǡ�����![]() �غϣ����Ե���
�غϣ����Ե���![]() ��
��![]() �е��˶�����Oʱ����
�е��˶�����Oʱ����![]() ǡ����ӵ�
ǡ����ӵ�![]() �˶�����M.
�˶�����M.
��ͼ��1������CH=3��HM=6����![]() ��
��
������![]() ����
����![]() ��
��
����BC�ӳ�����ȡ��K��ʹCK=CM=![]() ����
����![]() ����
����![]() ���������֪����Q�ij�������ǵ�K.
���������֪����Q�ij�������ǵ�K.
������ͼ1��ʾ��ƽ��ֱ������ϵ��
��PQ��OFʱ��PQ��DE��
��D��0��4����E��8��2������ֱ��DE�Ľ���ʽΪ��![]() ��������
��������![]() ������P��t��0������ã�
������P��t��0������ã�![]() ����
����![]() ��
��
��C��4��4����B��12��0������ֱ��BD�Ľ���ʽΪ��![]() ��
��
���������飺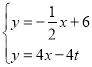 �����
�����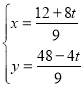 ��
��
���Q��![]() ��
��![]() ����
����
����Q��QR��y���ڵ�R����![]() ��
��
��ֱ����QRN�У�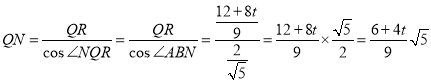 ��
��
��![]() ��
��
�ɢ�֪��![]() ����
����![]() =
=![]() ����ã�
����ã�![]() ��
��
��PQ��OEʱ����ͼ2��
��O��4��0����E��8��2������ֱ��OE�Ľ���ʽΪ��![]() ��
��
����ֱ��PQ�Ľ���ʽΪ��![]() ����P��t��0������ã�
����P��t��0������ã�![]() ��
��
��![]() ��
��
���������飺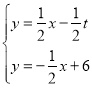 ����ã�
����ã�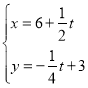 ����Q��
����Q��![]() ��
��![]() ����
����
����Q��QR��y���ڵ�R����![]() ��
��
��ֱ�ǡ�QRN�У�![]() ��
��
��![]() ��
��
�ɢ�֪��![]() ����
����![]() =
=![]() ����ã�
����ã�![]() ��
��
��Ȼ�ڵ�P���˶������У�PQ��DEʼ�ղ�ƽ�У�
���ϣ���![]() ��
��![]() ��һ��ƽ��ʱ��
��һ��ƽ��ʱ��![]() ��
��![]() .
.


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��ax2+bx+1�Ķ���ΪD����x�������ύ��A��B���㣬A��B����y�������ύ�ڵ�C������ABD�͡�OBC��Ϊ����ֱ�������Σ�OΪ����ԭ�㣩ʱ��b��ֵΪ��������

A. 2 B. ��2��4 C. ��2 D. ��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
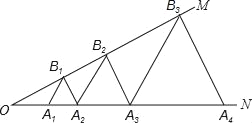
����Ŀ����ͼ����֪����MON=30�㣬��A1��A2��A3������ON�ϣ���B1��B2��B3��������OM�ϣ���A1B1A2����A2B2A3����A3B3A4����Ϊ�ȱ������Σ���OA1=1������A6B6A7�ı߳�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
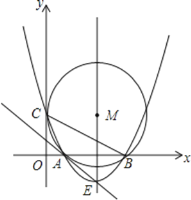
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���M�������ǣ�5��4������M��y�������ڵ�C����x���ཻ��A��B���㣮
��1����ֱ��д��A��B��C��������꣬�������������������߽���ʽ��
��2���裨1���������߽���ʽ�Ķ���ΪE��
��֤��ֱ��EA���M���У�
��3���������ߵĶԳ����ϣ��Ƿ���ڵ�P���ҵ�P��x����Ϸ���ʹ��PBC�ǵ��������Σ�
������ڣ��������P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
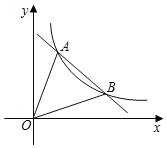
����Ŀ����ͼ��ʾ��˫����y��![]() ��x��0��k��0����ֱ��y��ax+b��a��0��bΪ����������A��2��4����B��m��2�����㣮
��x��0��k��0����ֱ��y��ax+b��a��0��bΪ����������A��2��4����B��m��2�����㣮
��1����m��ֵ��
��2����C������Ϊ��n��0������AC+BC��ֵ��Сʱ�����n��ֵ��
��3������AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������⼰����y=x��y=x2��y=![]()
�����![]() ����ô0��a��1��
����ô0��a��1��
�����![]() ����ôa��1��
����ôa��1��
�����![]() ����ô��1��a��0��
����ô��1��a��0��
�����![]() ʱ����ôa����1��
ʱ����ôa����1��
��
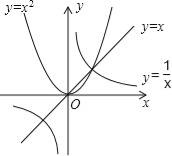
A.��ȷ���������٢�B.������������ڢۢ�
C.��ȷ���������٢�D.���������ֻ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�ַdz��ܻ�ӭ��ũ�����֪��ֲij�ִ�ƽ������Ϊ![]() ��/���꣬����ɱ�Ϊ8ǧԪ/���꣬ij�����۴ĵ���
��/���꣬����ɱ�Ϊ8ǧԪ/���꣬ij�����۴ĵ���![]() ǧԪ/������ֲ�����
ǧԪ/������ֲ�����![]() ����֮���ϵ��ͼ��ʾ��
����֮���ϵ��ͼ��ʾ��
Ϊ�˹���ũ����ֲ��ʳ�����飬��������̨������ߣ��Ա�����ֲ��ũ������4.5ǧԪ/�ֽ��в������������۵��۵���4.5ǧԪ/��ʱ������������ṩ�������������۵���Ϊ4ǧԪ/�֣�����������ũ��0.5ǧԪ/�֣������۲�����4.5ǧԪ/��ʱ����������
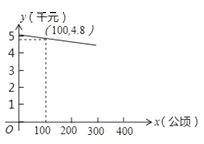
��1�������мƻ���ֲ��300���꣬���ۺ��Ƿ��������������������������ܲ����ܽ���Ƕ���ǧԪ��
��2����������۴�õ������������������֣�ΪwǧԪ������ֲ���Ϊ���ٹ���ʱ���������������Ƕ���ǧԪ��ע����������=�����۵�����ÿ�������-ÿ����ɱ�����������
��3��Ϊ��֤���õ����������ܵõ��������������ﵽ748ǧԪ��Ӧ����ֲ���ٹ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() ����
����![]() �ӵ�
�ӵ�![]() ��ʼ�ر�
��ʼ�ر�![]() ���յ�
���յ�![]() ��
��![]() ���ٶ��ƶ������ͬʱ����
���ٶ��ƶ������ͬʱ����![]() �ӵ�
�ӵ�![]() ��ʼ�ر�
��ʼ�ر�![]() ���յ�
���յ�![]() ��
��![]() ���ٶ��ƶ������
���ٶ��ƶ������![]() �ֱ��
�ֱ��![]() ͬʱ����������
ͬʱ����������![]() �˶�����
�˶�����![]() ʱ������ֹͣ�˶������˶�ʱ��Ϊ
ʱ������ֹͣ�˶������˶�ʱ��Ϊ![]() �룮
�룮

��1����գ�![]() __________��
__________��![]() _________�����ú�
_________�����ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() �ij��ȵ���
�ij��ȵ���![]() ��
��
��3����![]() Ϊ��ֵʱ�������
Ϊ��ֵʱ�������![]() ���������Сֵ����СֵΪ���٣�
���������Сֵ����СֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ���˽��һѧ������ˮ֪ʶ��������������ȡ���ֳ�һѧ�����������֪ʶ���ԣ����Է�ΪA��B��C��D�ĸ��ȼ�����ͳ�ƣ���ͳ�ƽ������������������������ͳ��ͼ��
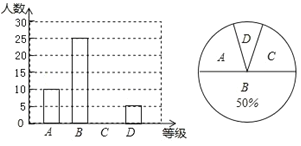
�����������⣺
(1)��У�μӱ��η���ˮ֪ʶ���Թ���______�ˣ�
(2)��ȫ����ͳ��ͼ��
(3)����У��һ�꼶����ѧ��1000�ˣ��Թ��Ƹ�Уѧ���жԷ���ˮ֪ʶ�������ܴﵽA����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com