
【题目】抛物线y=ax2+bx+1的顶点为D,与x轴正半轴交于A、B两点,A在B左,与y轴正半轴交于点C,当△ABD和△OBC均为等腰直角三角形(O为坐标原点)时,b的值为( )

A. 2 B. ﹣2或﹣4 C. ﹣2 D. ﹣4
【答案】D
【解析】
根据题意和函数图象,利用二次函数的性质和等腰三角形的性质,可以求得b的值,本题得以解决.
解:∵抛物线y=ax2+bx+1,
∴x=0时,y=1,
∴点C的坐标为(0,1),
∴OC=1,
∵△OBC为等腰直角三角形,
∴OC=OB,
∴OB=1,
∴抛物线y=ax2+bx+1与x轴的一个交点为(1,0),
∴a+b+1=0,得a=﹣1﹣b,
设抛物线y=ax2+bx+1与x轴的另一个交点A为(x1,0),
∴x1×1=![]() ,
,
∵△ABD为等腰直角三角形,
∴点D的纵坐标的绝对值是AB的一半,
∴![]() ,
,
∴![]() ,
,
解得,b=﹣2或b=﹣4,
当b=﹣2时,a=﹣1﹣(﹣2)=1,此时y=x2﹣2x+1=(x﹣1)2,与x轴只有一个交点,故不符合题意,
当b=﹣4时,a=﹣1﹣(﹣4)=3,此时y=3x2﹣4x+1,与x轴两个交点,符合题意,
故选:D.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
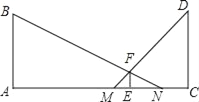
【题目】如图所示,晚上小亮走在大街上,他发现当他站在大街上高度相等的两盏路灯AB和CD之间时,自己右边的影子NE的长为3m,左边的影子ME的长为1.5m,又知小亮的身高EF为1.80m,两盏路灯AC之间的距离为12m,点A、M、E、N、C在同一条直线上,问:路灯的高为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 | 乙 | 丙 | |
平均数 | 7.9 | 7.9 | 8.0 |
方差 | 3.29 | 0.49 | 1.8 |
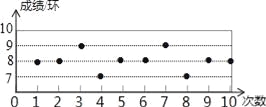
根据以上图表信息,参赛选手应选( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
![]()

(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24 g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个函数中,图象经过原点且对称轴在y轴左侧的二次函数是( )
A. y=x2+2x B. y=x2﹣2x C. y=2(x+1)2 D. y=2(x﹣1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
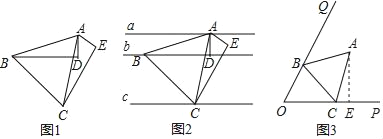
【题目】(1)如图1,△AEC中,∠E=90°,将△AEC绕点A顺时针旋转60°得到△ADB,AC与AB对应,AE与AD对应
①请证明△ABC为等边三角形;
②如图2,BD所在的直线为b,分别过点A、C作直线b的平行线a、c,直线a、b之间的距离为2,直线a、c之间的距离为7,则等边△ABC的边长为 .
(2)如图3,∠POQ=60°,△ABC为等边三角形,点A为∠POQ内部一点,点B、C分别在射线OQ、OP上,AE⊥OP于E,OE=5,AE=2![]() ,求△ABC的边长.
,求△ABC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
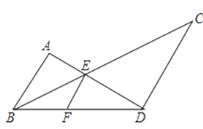
【题目】如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,
(1)图中有哪几对位似三角形,选其中一对加以证明;
(2)若AB=2,CD=3,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.根据图5中①所示的程序,得到了y与x的函数图象,如图5中②,若点M是
y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P、Q,连接OP、OQ,则以下结论:

①x<0时,y=![]()
②△OPQ的面积为定值
③x>0时,y随x的增大而增大
④MQ=2PM
⑤∠POQ可以等于90°
其中正确结论是
A.①②④B.②④⑤C.③④⑤D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
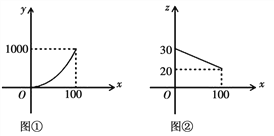
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用![]() 万元
万元![]() 与年产量
与年产量![]() 万件
万件![]() 之间的函数图象是顶点为原点的抛物线的一部分
之间的函数图象是顶点为原点的抛物线的一部分![]() 如图
如图![]() 所示
所示![]() ;该产品的销售单价
;该产品的销售单价![]() 元
元![]() 件
件![]() 与年销售量
与年销售量![]() 万件
万件![]() 之间的函数图象是如图
之间的函数图象是如图![]() 所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元
所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元![]() 毛利润
毛利润![]() 销售额
销售额![]() 生产费用
生产费用![]()
![]() 请写出y与x以及z与x之间的函数关系式;
请写出y与x以及z与x之间的函数关系式;
![]() 求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com