
【题目】.根据图5中①所示的程序,得到了y与x的函数图象,如图5中②,若点M是
y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P、Q,连接OP、OQ,则以下结论:

①x<0时,y=![]()
②△OPQ的面积为定值
③x>0时,y随x的增大而增大
④MQ=2PM
⑤∠POQ可以等于90°
其中正确结论是
A.①②④B.②④⑤C.③④⑤D.②③⑤
【答案】B
【解析】
由流程图可知函数解析式从而判断①;S△OPQ= S△PMQ+ S△MQO=1+2=3,可判断②;由图像可判断③;由流程图可知函数解析式:x<0时,y=![]() ;x>0时,y=
;x>0时,y=![]() ,再分别用OM表示PM和MQ即可证明;∠POQ=90°时,△PMO∽△OMQ,利用相似的性质可求解出PM、QM以及OM三者之间的关系,即PM、QM以及OM三者之间满足一定的数量关系可得到∠POQ=90°,据此判断⑤.
,再分别用OM表示PM和MQ即可证明;∠POQ=90°时,△PMO∽△OMQ,利用相似的性质可求解出PM、QM以及OM三者之间的关系,即PM、QM以及OM三者之间满足一定的数量关系可得到∠POQ=90°,据此判断⑤.
解:由流程图可知,x<0时,y=![]() ,故①错误;由反比例函数系数k的几何意义可得S△PMQ =1,S△MQO=2,则S△OPQ= S△PMQ+ S△MQO=1+2=3,故②正确;由图像可知,x>0时,y随x的增大而减小,故③错误;由流程图可知函数解析式:x<0时,y=
,故①错误;由反比例函数系数k的几何意义可得S△PMQ =1,S△MQO=2,则S△OPQ= S△PMQ+ S△MQO=1+2=3,故②正确;由图像可知,x>0时,y随x的增大而减小,故③错误;由流程图可知函数解析式:x<0时,y=![]() ;x>0时,y=
;x>0时,y=![]() ,则PM=
,则PM=![]() ,MQ=
,MQ=![]() ,则MQ=2PM,故④正确;∠POQ=90°时,△PMO∽△OMQ,则
,则MQ=2PM,故④正确;∠POQ=90°时,△PMO∽△OMQ,则![]() ,则可得OM2=PM×MQ,即当OM2=PM×MQ时,∠POQ=90°,故⑤正确.
,则可得OM2=PM×MQ,即当OM2=PM×MQ时,∠POQ=90°,故⑤正确.
故选择D.


科目:初中数学 来源: 题型:
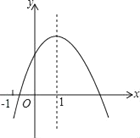
【题目】已知二次函数y=ax2+bx+c的图象如图,下列结论中,正确的结论的个数有( )
①a+b+c>0 ②a﹣b+c>0 ③abc<0 ④b+2a=0 ⑤△>0.
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+1的顶点为D,与x轴正半轴交于A、B两点,A在B左,与y轴正半轴交于点C,当△ABD和△OBC均为等腰直角三角形(O为坐标原点)时,b的值为( )

A. 2 B. ﹣2或﹣4 C. ﹣2 D. ﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“流感”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例(如图所示)。现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg。研究表明,当空气中每立方米的含药量不低于3mg才有效,那么此次消毒的有效时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
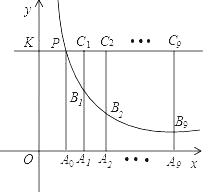
【题目】如图,直线y=k和双曲线y=![]() 相交于点P,过P点作PA0垂直x轴,垂足为A0,x轴上的点A0、A1、A2、…A9的横坐标是连续的整数,过点A1、A2、…A9分别作x轴的垂线,与双曲线y=
相交于点P,过P点作PA0垂直x轴,垂足为A0,x轴上的点A0、A1、A2、…A9的横坐标是连续的整数,过点A1、A2、…A9分别作x轴的垂线,与双曲线y=![]() (x>0)及直线y=k分别交于点B1、B2、…B9,C1、C2、…C9,则
(x>0)及直线y=k分别交于点B1、B2、…B9,C1、C2、…C9,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学三次到某超市购买A、B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:
类别 次数 | 购买A商品数量(件) | 购买B商品数量(件) | 消费金额(元) |
第一次 | 4 | 5 | 320 |
第二次 | 2 | 6 | 300 |
第三次 | 5 | 7 | 258 |
解答下列问题:
(1)第 次购买有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买A、B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元,求至少购买A商品多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
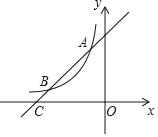
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求a,k的值及点B的坐标;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,直接写出点P的坐标.
S△BOC,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+mx+n的图象经过点P(﹣3,1),对称轴是直线x=﹣1.
(1)求m,n的值;
(2)x取什么值时,y随x的增大而减小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com