
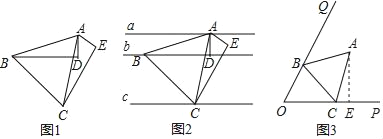
°ĺŐ‚ńŅ°Ņ£®1£©»ÁÕľ1£¨°ųAEC÷–£¨°ŌE£Ĺ90°„£¨Ĺę°ųAEC»∆Ķ„Aň≥ Ī’Ž–ż◊™60°„Ķ√ĶĹ°ųADB£¨AC”ŽAB∂‘”¶£¨AE”ŽAD∂‘”¶
ĘŔ«Ž÷§√ų°ųABCő™Ķ»ĪŖ»żĹ«–ő£Ľ
Ęŕ»ÁÕľ2£¨BDňý‘ŕĶń÷ĪŌŖő™b£¨∑÷ĪūĻżĶ„A°ĘC◊ų÷ĪŌŖbĶń∆Ĺ––ŌŖa°Ęc£¨÷ĪŌŖa°Ęb÷ģľšĶńĺŗņŽő™2£¨÷ĪŌŖa°Ęc÷ģľšĶńĺŗņŽő™7£¨‘ÚĶ»ĪŖ°ųABCĶńĪŖ≥§ő™°° °°£ģ
£®2£©»ÁÕľ3£¨°ŌPOQ£Ĺ60°„£¨°ųABCő™Ķ»ĪŖ»żĹ«–ő£¨Ķ„Aő™°ŌPOQńŕ≤Ņ“ĽĶ„£¨Ķ„B°ĘC∑÷Īū‘ŕ…šŌŖOQ°ĘOP…Ō£¨AE°ÕOP”ŕE£¨OE£Ĺ5£¨AE£Ĺ2![]() £¨«ů°ųABCĶńĪŖ≥§£ģ
£¨«ů°ųABCĶńĪŖ≥§£ģ
°ĺīūįł°Ņ£®1£©ĘŔŌÍľŻĹ‚őŲ£ĽĘŕ![]() £Ľ£®2£©
£Ľ£®2£©![]() .
.
°ĺĹ‚őŲ°Ņ
£®1£©”…–ż◊™Ķń–‘÷ Ņ…Ķ√£ļAB£ĹAC£¨°ŌBAC£Ĺ60°„£¨ľīŅ…÷§°ųABCő™Ķ»ĪŖ»żĹ«–ő£Ľ
£®2£©ĻżĶ„E◊ųEG°Õ÷ĪŌŖa£¨—”≥§GEĹĽ÷ĪŌŖc”ŕĶ„H£¨Ņ…Ķ√GH£Ĺ7£¨AD£Ĺ2£¨”…–ż◊™Ķń–‘÷ Ņ…Ķ√AD£ĹAE£Ĺ2£¨°ŌDAE£Ĺ60°„£¨Ņ…«ůGE£Ĺ1£¨EH£Ĺ6£¨”…»ŮĹ«»żĹ«ļĮ żŅ…«ůCE£Ĺ4![]() £¨łýĺ›ĻīĻ…∂®ņŪŅ…«ůĶ»ĪŖ°ųABCĶńĪŖACĶń≥§£Ľ
£¨łýĺ›ĻīĻ…∂®ņŪŅ…«ůĶ»ĪŖ°ųABCĶńĪŖACĶń≥§£Ľ
£®3£©ĻżĶ„A◊ų°ŌAHO£Ĺ60°„£¨ĹĽOQ”ŕĶ„G£¨ĹĽOP”ŕĶ„H£¨łýĺ›Őō ‚»żĹ«ļĮ ż÷ĶŅ…«ůAH£Ĺ4£¨Õ®Ļż÷§√ų°ųOBC°’°ųHCA£¨Ņ…«ůAH£ĹOC£Ĺ4£¨CE£Ĺ1£¨łýĺ›ĻīĻ…∂®ņŪŅ…«ů°ųABCĶńĪŖACĶń≥§£ģ
Ĺ‚£ļ£®1£©°ŖĹę°ųAEC»∆Ķ„Aň≥ Ī’Ž–ż◊™60°„Ķ√ĶĹ°ųADB£¨
°ŗAB£ĹAC£¨°ŌBAC£Ĺ60°„£¨
°ŗ°ųABCő™Ķ»ĪŖ»żĹ«–ő£ģ
£®2£©ĻżĶ„E◊ųEG°Õ÷ĪŌŖa£¨—”≥§GEĹĽ÷ĪŌŖc”ŕĶ„H£¨
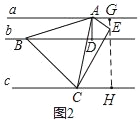
°Ŗa°őb°őc£¨
°ŗEH°Õ÷ĪŌŖc£¨
°Ŗ÷ĪŌŖa°Ęc÷ģľšĶńĺŗņŽő™7£¨
°ŗGH£Ĺ7
°ŖĹę°ųAEC»∆Ķ„Aň≥ Ī’Ž–ż◊™60°„Ķ√ĶĹ°ųADB£¨
°ŗAD£ĹAE£¨°ŌADB£Ĺ°ŌAEC£Ĺ90°„£¨°ŌDAE£Ĺ60°„£¨
°Ŗ÷ĪŌŖa°Ęb÷ģľšĶńĺŗņŽő™2£¨
°ŗAD£Ĺ2£ĹAE£¨
°Ŗ°ŌGAE£Ĺ°ŌGAD©Ā°ŌDAE£Ĺ90°„©Ā60°„£Ĺ30°„£¨
°ŗGE£Ĺ![]() AE£Ĺ1£¨°ŌAEG£Ĺ60°„£¨
AE£Ĺ1£¨°ŌAEG£Ĺ60°„£¨
°ŗEH£Ĺ7©Ā1£Ĺ6£¨
°Ŗ°ŌCEH£Ĺ180°„©Ā°ŌAEC©Ā°ŌAEG£¨
°ŗ°ŌCEH£Ĺ30°„£¨
°ŗcos°ŌCEH£Ĺ![]() £¨
£¨
°ŗCE£Ĺ4![]()
‘ŕRt°ųACE÷–£¨AC£Ĺ![]() £Ĺ
£Ĺ![]() £Ĺ2
£Ĺ2![]() £¨
£¨
Ļ īūįłő™£ļ2![]()
£®3£©ĻżĶ„A◊ų°ŌAHO£Ĺ60°„£¨ĹĽOQ”ŕĶ„G£¨ĹĽOP”ŕĶ„H£¨
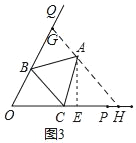
°ŖAE°ÕOP£¨°ŌAHO£Ĺ60°„
°ŗsin°ŌAHO£Ĺ![]()
°ŗAH£Ĺ4
°Ŗ°ųABC «Ķ»ĪŖ»żĹ«–ő£¨
°ŗAB£ĹAC£ĹBC£¨°ŌACB£Ĺ60°„£Ĺ°ŌPOQ£¨
°Ŗ°ŌPOQ+°ŌOBC+°ŌOCB£Ĺ180°„£¨°ŌACB+°ŌOCB+°ŌACH£Ĺ180°„£¨
°ŗ°ŌACH£Ĺ°ŌOBC£¨«“BC£ĹAC£¨°ŌO£Ĺ°ŌAHC£Ĺ60°„£¨
°ŗ°ųOBC°’°ųHCA£®AAS£©
°ŗAH£ĹOC£Ĺ4£¨
°ŗCE£ĹOE©ĀOC£Ĺ5©Ā4£Ĺ1£¨
‘ŕRt°ųACE÷–£¨AC£Ĺ![]() £Ĺ
£Ĺ![]() £Ĺ
£Ĺ![]() £¨
£¨
°ŗ°ųABCĶńĪŖ≥§ő™![]() £ģ
£ģ



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨∂ĢīőļĮ ż![]() ĶńÕľŌŮĺ≠ĻżĶ„
ĶńÕľŌŮĺ≠ĻżĶ„![]() ,”Ž
,”Ž![]() ÷ŠĹĽ”ŕĶ„
÷ŠĹĽ”ŕĶ„![]() ,
,![]() °Ę
°Ę![]() ∑÷Īūő™
∑÷Īūő™![]() ÷Š°Ę÷ĪŌŖ
÷Š°Ę÷ĪŌŖ![]() …ŌĶń∂ĮĶ„,ĶĪňńĪŖ–ő
…ŌĶń∂ĮĶ„,ĶĪňńĪŖ–ő![]() Ķń÷‹≥§◊Ó–° Ī,
Ķń÷‹≥§◊Ó–° Ī,![]() ňý‘ŕ÷ĪŌŖ∂‘”¶ĶńļĮ żĪŪīÔ Ĺ «( )
ňý‘ŕ÷ĪŌŖ∂‘”¶ĶńļĮ żĪŪīÔ Ĺ «( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™Ļō”ŕxĶń“Ľ‘™∂Ģīő∑Ĺ≥Őax2©Ā£®a+2£©x+2=0”–ŃĹłŲ≤ĽŌŗĶ»Ķń’ż’Ż żłý Ī£¨’Ż żaĶń÷Ķ «_____£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ°—O÷–£¨AB «÷Īĺ∂£¨CD «Ō“£¨AB°ÕCD£ģ
£®1£©P «![]() …Ō“ĽĶ„£®≤Ľ”ŽC°ĘD÷ōļŌ£©£¨«ů÷§£ļ°ŌCPD=°ŌCOB£Ľ
…Ō“ĽĶ„£®≤Ľ”ŽC°ĘD÷ōļŌ£©£¨«ů÷§£ļ°ŌCPD=°ŌCOB£Ľ
£®2£©Ķ„P°š‘ŕŃ”Ľ°CD…Ō£®≤Ľ”ŽC°ĘD÷ōļŌ£© Ī£¨°ŌCP°šD”Ž°ŌCOB”– ≤√ī żŃŅĻōŌĶ£Ņ«Ž÷§√ųń„ĶńĹŠ¬Ř£ģ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
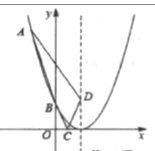
°ĺŐ‚ńŅ°ŅŇ◊őÔŌŖy£Ĺax2+bx+1Ķń∂•Ķ„ő™D£¨”Žx÷Š’żįŽ÷ŠĹĽ”ŕA°ĘBŃĹĶ„£¨A‘ŕB◊ů£¨”Žy÷Š’żįŽ÷ŠĹĽ”ŕĶ„C£¨ĶĪ°ųABDļÕ°ųOBCĺýő™Ķ»—Ł÷ĪĹ«»żĹ«–ő£®Oő™◊ÝĪÍ‘≠Ķ„£© Ī£¨bĶń÷Ķő™£®°°°°£©

A. 2 B. ©Ā2ĽÚ©Ā4 C. ©Ā2 D. ©Ā4
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“Ľň“”śī¨őĽ”ŕłŘŅŕAĶńĪĪ∆ę∂ę60°„∑ĹŌÚ£¨ĺŗņŽłŘŅŕ20ļ£ņÔĶńBī¶£¨ňŁ—ōĪĪ∆ęőų37°„∑ĹŌÚļĹ––÷ŃCī¶ÕĽ»Ľ≥ŲŌ÷Ļ ’Ō£¨‘ŕCī¶Ķ»īżĺ»‘ģ£¨B£¨C÷ģľšĶńĺŗņŽő™10ļ£ņÔ£¨ĺ»‘ģī¨ī”łŘŅŕA≥Ų∑Ę£¨ĺ≠Ļż20∑÷÷”ĶĹīÔCī¶£¨«ů廑ģī¨ĶńļĹ––ňŔ∂»£ģ(sin37°„°÷0.6£¨cos37°„°÷0.8£¨![]() °÷1.732£¨ĹŠĻŻ»°’Ż ż)
°÷1.732£¨ĹŠĻŻ»°’Ż ż)
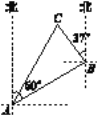
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ «ń≥–°«ÝĶń“ĽłŲĹ°…Ū∆ų≤ń£¨“—÷™BC=0.15m£¨AB=2.70m£¨°ŌBOD=70°„£¨«ů∂ňĶ„AĶĹĶō√śCDĶńĺŗņŽ£®ĺę»∑ĶĹ0.1m£©£ģ£®≤őŅľ żĺ›£ļsin70°„°÷0.94£¨cos70°„°÷0.34£¨tan70°„°÷2.75£©

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
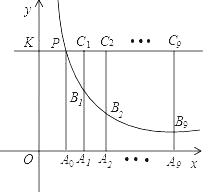
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨÷ĪŌŖy£ĹkļÕňę«ķŌŖy£Ĺ![]() ŌŗĹĽ”ŕĶ„P£¨ĻżPĶ„◊ųPA0īĻ÷Īx÷Š£¨īĻ◊„ő™A0£¨x÷Š…ŌĶńĶ„A0°ĘA1°ĘA2°Ę°≠A9ĶńļŠ◊ÝĪÍ «Ń¨–ÝĶń’Ż ż£¨ĻżĶ„A1°ĘA2°Ę°≠A9∑÷Īū◊ųx÷ŠĶńīĻŌŖ£¨”Žňę«ķŌŖy£Ĺ
ŌŗĹĽ”ŕĶ„P£¨ĻżPĶ„◊ųPA0īĻ÷Īx÷Š£¨īĻ◊„ő™A0£¨x÷Š…ŌĶńĶ„A0°ĘA1°ĘA2°Ę°≠A9ĶńļŠ◊ÝĪÍ «Ń¨–ÝĶń’Ż ż£¨ĻżĶ„A1°ĘA2°Ę°≠A9∑÷Īū◊ųx÷ŠĶńīĻŌŖ£¨”Žňę«ķŌŖy£Ĺ![]() £®x£ĺ0£©ľį÷ĪŌŖy£Ĺk∑÷ĪūĹĽ”ŕĶ„B1°ĘB2°Ę°≠B9£¨C1°ĘC2°Ę°≠C9£¨‘Ú
£®x£ĺ0£©ľį÷ĪŌŖy£Ĺk∑÷ĪūĹĽ”ŕĶ„B1°ĘB2°Ę°≠B9£¨C1°ĘC2°Ę°≠C9£¨‘Ú![]() £Ĺ_____£ģ
£Ĺ_____£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ,‘ŕĪŖ≥§ő™1łŲĶ•őĽ≥§∂»Ķń–°’ż∑Ĺ–ő◊ť≥…ĶńÕÝłŮ÷–,įī“™«ůÕÍ≥…Ō¬√śĶńő Ő‚:
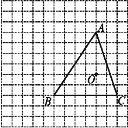
(1)“‘Õľ÷–ĶńOő™őĽň∆÷––ń,Ĺę°ųABC◊ųőĽň∆ĪšĽĽ«“ňű–°ĶĹ‘≠ņīĶń“ĽįŽ,Ķ√ĶĹ°ųA'B'C',‘Ŕį—°ųA'B'C'»∆Ķ„B'ńś Ī’Ž–ż◊™90°„Ķ√ĶĹ°ųA°ŚB'C°Ś;
(2)«ůĶ„A°ķA'°ķA°Śňýĺ≠ĻżĶń¬∑ŌŖ≥§.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com