[题目]相传有个人不讲究说话艺术常引起误会.一天他摆宴席请客.他看到还有几个人没来.就自言自语:“怎么该来的还不来啊? 客人听了心里想难道我们是不该来的.于是有一半客人走了．他一看十分着急.又说:“不该走的倒走了! 剩下的人一听.是我们该走啊!又有剩下的三分之二的人离开了．他着急地一拍大腿.连说:“我说的不是他们．于是题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】相传有个人不讲究说话艺术常引起误会，一天他摆宴席请客，他看到还有几个人没来，就自言自语：“怎么该来的还不来啊？”客人听了心里想难道我们是不该来的，于是有一半客人走了．他一看十分着急，又说：“不该走的倒走了！”剩下的人一听，是我们该走啊！又有剩下的三分之二的人离开了．他着急地一拍大腿，连说：“我说的不是他们．”于是最后剩下的四个人也都告辞走了．聪明的你能知道刚开始来的客人个数是(　　)

A. 24 B. 18 C. 16 D. 15

【答案】A

【解析】

可以设原来有x人，第一批走了x，第二批走了（x-x），剩下四人，以人数为等量关系可列方程求解．

解：设原来有x人，

x+（x-x）+4=x，

x=24，

∴开始来了24个客人．

故选：A．

练习册系列答案

中考导学案系列答案

中考大提速系列答案

中考专题通系列答案

中考第三轮复习冲刺专用模拟试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】自学下面材料后，解答问题

分母中含有未知数的不等式叫做分式不等式，如：；等那么如何求出它们的解集呢？

根据我们学过的有理数除法法则可知：两数相除，同号得正，异号得负其字母表达式为：

若，，则；若，，则

反之：若，则或

若，则______或______．

根据上述规律

求不等式的解集．

直接写出一个解集为或的最简分式不等式．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．

原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，

连接EF，则EF=BE+DF，试说明理由．

（1）思路梳理

∵AB=AD

∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合

∵∠ADC=∠B=90°

∴∠FDG=180°

∴点F、D、G共线

根据，易证△AFG≌ ，进而得EF=BE+DF．

（2）联想拓展

如图2，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°．猜想BD、DE、EC应满足的数量关系，并写出推理过程．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知抛物线y=ax2+bx+c的图象如图所示，则一元二次方程ax2+bx+c=0（）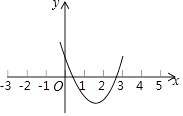

A.没有实根
B.只有一个实根
C.有两个实根，且一根为正，一根为负
D.有两个实根，且一根小于1，一根大于2

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在有些情况下，不需要计算出结果也能把绝对值符号去掉．例如：

|6＋7|＝6＋7；|6－7|＝7－6；|7－6|＝7－6；|－6－7|＝6＋7；

根据上面的规律，把下列各式写成去掉绝对值符号的形式：

(1)|7－21|＝_________；

(2)||＝____________；

(3)||＝__________；

(4)用合理的方法计算：||＋||－×|－|＋.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在同一平面内，△ABC和△ABD如图①放置，其中AB=BD．
小明做了如下操作：
将△ABC绕着边AC的中点旋转180°得到△CEA，将△ABD绕着边AD的中点旋转180°得到△DFA，如图②，请完成下列问题：

（1）试猜想四边形ABDF是什么特殊四边形，并说明理由；
（2）连接EF，CD，如图③，求证：四边形CDEF是平行四边形．