
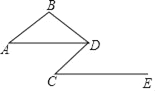
【题目】如图,已知AB∥CD,DA平分∠BDC,∠A=∠C.
(1)试说明:CE∥AD;
(2)若∠C=30°,求∠B的度数.
 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
【题目】相传有个人不讲究说话艺术常引起误会,一天他摆宴席请客,他看到还有几个人没来,就自言自语:“怎么该来的还不来啊?”客人听了心里想难道我们是不该来的,于是有一半客人走了.他一看十分着急,又说:“不该走的倒走了!”剩下的人一听,是我们该走啊!又有剩下的三分之二的人离开了.他着急地一拍大腿,连说:“我说的不是他们.”于是最后剩下的四个人也都告辞走了.聪明的你能知道刚开始来的客人个数是( )
A. 24 B. 18 C. 16 D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD中,AB=6,∠B=60°.E是BC边上一动点,F是CD边上一动点,且BE=CF,连接AE、AF.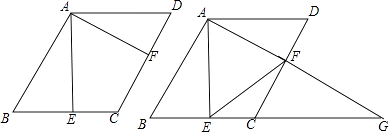
(1)∠EAF的度数是;
(2)求证:AE=AF;
(3)延长AF交BC的延长线于点G,连接EF,设BE=x,EF2=y,求y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级学生开展测量物体高度的实践活动,他们要测量学校一幢教学楼的高度,如图,他们先在点C测得教学楼AB的顶点A的仰角为30°,然后向教学楼前进20米到达点D,又测得点A的仰角为45°,请根据这些数据,求这幢教学楼的高度.(最后结果精确到1米,参考数据 ![]() ≈1.732)
≈1.732) 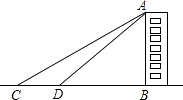
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司拟为贫困山区建一所希望小学,甲、乙两个工程队提交了投标方案,若独立完成该项目,则甲工程队所用时间是乙工程队的1.5倍;若甲、乙两队合作完成该项目,则共需72天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)若由甲工程队单独施工,平均每天的费用为0.8万元,为了缩短工期,该公司选择了乙工程队,但要求其施工的总费用不能超过甲工程队,求乙工程队平均每天的施工费用最多为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数y= ![]() 的图象上,过点A,B作x轴的垂线,垂足分别是M,N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
的图象上,过点A,B作x轴的垂线,垂足分别是M,N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( ) 
A.2
B.4
C.﹣2
D.﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴交与点E,已知点B(﹣1,0).
(1)点A的坐标: , 点E的坐标:;
(2)若二次函数y=﹣ ![]() x2+bx+c过点A、E,求此二次函数的解析式;
x2+bx+c过点A、E,求此二次函数的解析式;
(3)P是AC上的一个动点(P与点A、C不重合)连结PB、PD,设l是△PBD的周长,当l取最小值时,求点P的坐标及l的最小值并判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由.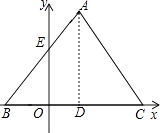
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE= ![]() AC,连接CE,OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
AC,连接CE,OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com