
【题目】如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE= ![]() AC,连接CE,OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
AC,连接CE,OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:在菱形ABCD中,OC= ![]() AC,AC⊥BD,
AC,AC⊥BD,
∴DE=OC,
∵DE∥AC,
∴四边形OCED是平行四边形,
∵AC⊥BD,
∴平行四边形OCED是矩形,
∵在菱形ABCD中,∠ABC=60°,
∴△ABC为等边三角形,
∴AD=AB=AC=2,OA= ![]() AC=1,
AC=1,
在矩形OCED中,由勾股定理得:CE=OD= ![]() =
= ![]() =
= ![]() ,
,
在Rt△ACE中,由勾股定理得:AE= ![]() =
= ![]() =
= ![]() ;
;
故选:C.
【考点精析】关于本题考查的菱形的性质,需要了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣4x与x轴交于点O,A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( ) 
A.4
B.8
C.16
D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】著名的瑞士数学家欧拉曾指出:可以表示为四个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为四个整数平方之和,即![]()
![]() ,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可减弱为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可减弱为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
【动手一试】
试将![]() 改成两个整数平方之和的形式.
改成两个整数平方之和的形式. ![]() ;
;
【阅读思考】
在数学思想中,有种解题技巧称之为“无中生有”.例如问题:将代数式![]() 改成两个平方之差的形式.解:原式
改成两个平方之差的形式.解:原式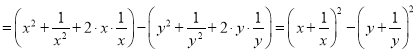 ﹒
﹒
【解决问题】
请你灵活运用利用上述思想来解决“不变心的数”问题:将代数式![]() 改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列哪组条件能够判别四边形ABCD是平行四边形?( )
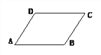
A. AB∥CD,AD=BC B. AB=CD,AD=BC
C. ∠A=∠B,∠C=∠D D. AB=AD,CB=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,延长CB到点M,使BM=1,连接AM,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为 . 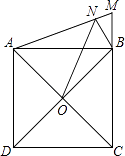
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:
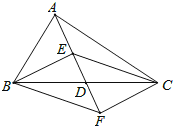
①BE⊥EC;②BF∥CE;③AB=AC;
从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,己知O为坐标原点,点A(3,0),B(0,4),以点A为旋转中心,把△ABO顺时针旋转,得△ACD.记旋转角为α.∠ABO为β.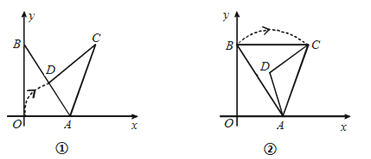
(Ⅰ)如图①,当旋转后点D恰好落在AB边上时,求点D的坐标;
(Ⅱ)如图②,当旋转后满足BC∥x轴时,求α与β之间的数量关系:
(Ⅲ)当旋转后满足∠AOD=β时,求直线CD的解析式(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com