
����Ŀ��̽����֪��
��ͼ1������OC��![]() ���ڲ���ͼ�й���3���ǣ�
���ڲ���ͼ�й���3���ǣ�![]() ��
��![]() ��
��![]() ����������һ���ǵĶ�������һ���Ƕ������������������OC��
����������һ���ǵĶ�������һ���Ƕ������������������OC��![]() �ġ��ɷ��ߡ���
�ġ��ɷ��ߡ���
��1��һ���ǵ�ƽ����______����ǵġ��ɷ��ߡ���![]() ��ǡ����ǡ�
��ǡ����ǡ�![]()
��2����ͼ2����![]() ��������PQ��
��������PQ��![]() �ġ��ɷ��ߡ�����
�ġ��ɷ��ߡ�����![]() ______��
______��![]() �ú�
�ú�![]() �Ĵ���ʽ��ʾ�����п��ܵĽ��
�Ĵ���ʽ��ʾ�����п��ܵĽ��![]()
�������
��ͼ2����![]() ��������PQ�Ƶ�P��PNλ�ÿ�ʼ����ÿ��
��������PQ�Ƶ�P��PNλ�ÿ�ʼ����ÿ��![]() ���ٶ���ʱ����ת����PQ��PN��
���ٶ���ʱ����ת����PQ��PN��![]() ʱֹͣ��ת����ת��ʱ��Ϊt�룮
ʱֹͣ��ת����ת��ʱ��Ϊt�룮
��3����tΪ��ֵʱ������PM��![]() �ġ��ɷ��ߡ���
�ġ��ɷ��ߡ���
��4��������PMͬʱ�Ƶ�P��ÿ��![]() ���ٶ���ʱ����ת������PQͬʱֹͣ����ֱ��д��������PQ��
���ٶ���ʱ����ת������PQͬʱֹͣ����ֱ��д��������PQ��![]() �ġ��ɷ��ߡ�ʱt��ֵ��
�ġ��ɷ��ߡ�ʱt��ֵ��



���𰸡��� ![]() ��
��![]() ��
��![]()
��������
![]() �����ɷ��߶��弴����⣻
�����ɷ��߶��弴����⣻
![]() ��3������������ɷ��߶��弴����⣻
��3������������ɷ��߶��弴����⣻
![]() ��3������������ɷ��߶���õ�������⼴�ɣ�
��3������������ɷ��߶���õ�������⼴�ɣ�
![]() ��3������������ɷ��߶���õ�������⼴�ɣ�
��3������������ɷ��߶���õ�������⼴�ɣ�
![]() һ���ǵ�ƽ����������ǵġ��ɷ��ߡ���
һ���ǵ�ƽ����������ǵġ��ɷ��ߡ���![]() ��ǡ����ǡ�
��ǡ����ǡ�![]()
�ʴ�Ϊ����
![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
�ʴ�Ϊ![]() ��
��![]() ��
��![]() ��
��
�������
![]() ��������
��������
![]() ��
��
���![]() ��
��
![]() ��
��
���![]() ��
��
![]() ��
��
���![]() ��
��
�ʵ�tΪ9��12��18ʱ������PM��![]() �ġ��ɷ��ߡ���
�ġ��ɷ��ߡ���
![]() ��������
��������
![]() ��
��
���![]() ��
��
![]() ��
��
���![]() ��
��
![]() ��
��
���![]() ��
��
�ʵ�tΪ![]() ��4��6ʱ������PQ��
��4��6ʱ������PQ��![]() �ġ��ɷ��ߡ���
�ġ��ɷ��ߡ���


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ1��С�����ι��ɵ������У��뾶Ϊ1�ġ�O��Բ��O�ڸ���ϣ����AED������ֵ���ڣ� �� 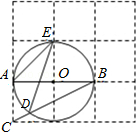
A.![]()
B.![]()
C.2
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
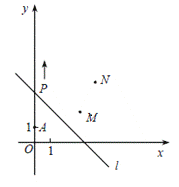
����Ŀ����ͼ��A��0��1����M��3��2����N��4��4��.����P�ӵ�A��������![]() ����ÿ��1����λ�����ٶ������ƶ����ҹ���P��ֱ��
����ÿ��1����λ�����ٶ������ƶ����ҹ���P��ֱ��![]() Ҳ��֮�ƶ������ƶ�ʱ��Ϊ
Ҳ��֮�ƶ������ƶ�ʱ��Ϊ![]() ��.
��.
��1����![]() ʱ����ֱ�ߵĽ���ʽ��
ʱ����ֱ�ߵĽ���ʽ��
��2������M��Nλ��ֱ�ߵ���࣬ȷ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��B��C�������϶�Ӧ��ʵ���ֱ�Ϊa��b��c�����㣨b+5��2+|a��8|=0����Pλ�ڸ������ϣ�
��1�����a��b��ֵ������A��B�����ľ��룻
��2�����C���A�ľ���Ϊ25����λ���ȣ���|ac|=��ac����PB=2PC�����P�������϶�Ӧ��ʵ����
��3������P��ԭ�㿪ʼ��һ�������ƶ�1����λ���ȣ��ڶ��������ƶ�3����λ���ȣ������������ƶ�5����λ���ȣ����Ĵ������ƶ�7����λ���ȣ������Դ����ƣ������p ���ƶ������A���B�غϵ�λ�������ܣ���̽����Ҫ�ƶ����ٴ��غϣ������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������6�֣�ij�ж�һ���ͳ������۵ļס��ҡ���3�ִ�����������⣮��������200��������������ΪA��B�����ȼ���A������B��������Ӧ���ݵ�ͳ��ͼ���£�
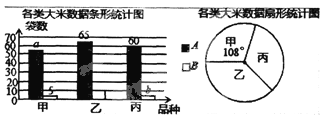
����������Ϣ������������⣺
(1)a��_______��b��_______��
(2)��֪�ó����������ִ���750�������ݼ������������Ƹó������ִ������ж��ٴ�B�����ף�
(3)���ڸó��еļ��ֺͱ��ִ��ף����ѡ������һ�֣���������ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���ACB=90�㣬CD��AB��D��AC=20��BC=15�� 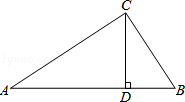
��1����AB�ij���
��2����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������x�ύ��A��B���㣬��y�ύC�㣬��A������Ϊ��2��0������C������Ϊ��0��3�����ĶԳ�����ֱ��x= ![]() ��
��
��1���������ߵĽ���ʽ��
��2��M���߶�AB�ϵ�����һ�㣬����MBCΪ����������ʱ����M������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ���x2+2��m��2��x+m2��3m+3=0��
��1������������ȵ�ʵ��������m��ȡֵ��Χ��
��2����x1��x2�Ƿ��̵�������x12+x22=6����mֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������⣺
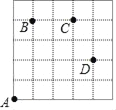
��ͼ��һֻ�׳���5��5�ķ���ÿ������߳���Ϊ1�����������������У������ǹ涨������ͼ�����У����ϣ������ң� ���м�Ϊ��+�������£������� ���м�Ϊ�����������ҵ�һ������ʾ���ҷ��ڶ�������ʾ���·���
���磺��A��B��Ϊ��A��B��+1��+4������D��C��Ϊ��D��C����1��+2����
˼����Ӧ�ã�
��1��ͼ��A��C���� ������ ������B��C���� ������ ������D��A���� ������ ����
��2�����׳��A��P������·������Ϊ����+3��+2������+1��+3������+1����2��������ͼ�б��P��λ�ã�
��3�����׳������·��ΪA����+1��+4������+2��0������+1����2��������4����2���������ü׳��߹�����·�̣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com