
【题目】关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0.
(1)有两个不相等的实数根,求m的取值范围;
(2)若x1,x2是方程的两根且x12+x22=6,求m值.
【答案】(1)m<1;(2)![]() .
.
【解析】试题分析:(1)由方程有两个不相等的实数根结合根的判别式,即可得出关于m的一元一次不等式,解之即可得出m的取值范围;
(2)根据根与系数的关系结合x12+x22=6,可得出关于m的一元二次方程,解之即可得出m的值,再结合(1)即可确定m的值.
试题解析:解:(1)∵方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根,∴△=[2(m﹣2)]2﹣4(m2﹣3m+3)=﹣4m+4>0,∴m<1.
(2)∵x1,x2是方程x2+2(m﹣2)x+m2﹣3m+3=0的两根,∴x1+x2=﹣2(m﹣2),x1x2=m2﹣3m+3.
∵x12+x22=6,∴(x1+x2)2﹣2x1x2=6,即[﹣2(m﹣2)]2﹣2(m2﹣3m+3)=6,解得:m1= ![]() (舍去),m2=
(舍去),m2= ![]() ,∴m的值为
,∴m的值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】红星中学九年级(1)班三位教师决定带领本班![]() 名学生利用假期去某地旅游,枫江旅行社的收费标准为:教师全价,学生半价;而东方旅行社不管教师还是学生一律八折优惠,这两家旅行社的全价都是500元。
名学生利用假期去某地旅游,枫江旅行社的收费标准为:教师全价,学生半价;而东方旅行社不管教师还是学生一律八折优惠,这两家旅行社的全价都是500元。
(1)用含![]() 的式子表示三位教师和
的式子表示三位教师和![]() 位学生参加这两家旅行社所需的费用各是多少元;
位学生参加这两家旅行社所需的费用各是多少元;
(2)如果![]() =50时,请你计算选择哪一家旅行社较为合算?
=50时,请你计算选择哪一家旅行社较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索新知:
如图1,射线OC在![]() 的内部,图中共有3个角:
的内部,图中共有3个角:![]() ,
,![]() 和
和![]() ,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是
,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是![]() 的“巧分线”.
的“巧分线”.
(1)一个角的平分线______这个角的“巧分线”;![]() 填“是”或“不是”
填“是”或“不是”![]()
(2)如图2,若![]() ,且射线PQ是
,且射线PQ是![]() 的“巧分线”,则
的“巧分线”,则![]() ______;
______;![]() 用含
用含![]() 的代数式表示出所有可能的结果
的代数式表示出所有可能的结果![]()
深入研究:
如图2,若![]() ,且射线PQ绕点P从PN位置开始,以每秒
,且射线PQ绕点P从PN位置开始,以每秒![]() 的速度逆时针旋转,当PQ与PN成
的速度逆时针旋转,当PQ与PN成![]() 时停止旋转,旋转的时间为t秒.
时停止旋转,旋转的时间为t秒.
(3)当t为何值时,射线PM是![]() 的“巧分线”;
的“巧分线”;
(4)若射线PM同时绕点P以每秒![]() 的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是
的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是![]() 的“巧分线”时t的值.
的“巧分线”时t的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科学技术协会为倡导青少年主动进行研究性学习,积极研究身边的科学问题,组织了以“体验、创新、成长”为主题的青少年科技创大赛,在层层选拔的基础上,所有推荐参赛学生分别获得了一、二、三等奖和纪念奖,工作人员根据获奖情况绘制成如图所示的两幅不完整的统计图,根据图中所给出的信息解答下列问题: 
(1)这次大赛获得三等奖的学生有多少人?
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示三等奖扇形的圆心角是多少度?
(4)若给所有推荐参赛学生每人发一张相同的卡片,各自写上自己的名字,然后把卡片放入一个不透明的袋子里,摇匀后任意摸出一张,求摸出写有一等奖学生名字卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x1、x2是一元二次方程2x2﹣7x+5=0的两根,利用一元二次方程根与系数的关系,求下列各式的值.
(1)x12x2+x1x22; (2)(x1﹣x2)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAE,交BF于C. 
(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)求证:AD=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(1)求一次函数,反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了统计知识后,班主任王老师叫班长就本班同学的上学方式进行了一次调查统计,图1和图2是他通过收集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题: 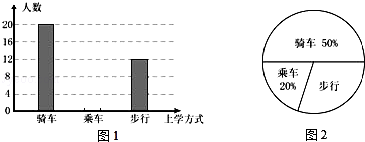
(1)在扇形统计图中,计算出“步行”部分所对应的圆心角的度数;
(2)求该班共有多少名学生;
(3)在图1中,将表示“乘车”的部分补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com