
【题目】如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
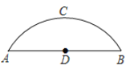
(1)求拱桥的半径;
(2)有一艘宽为5m的货船,船舱顶部为长方形,并高出水面3.4m,则此货船是否能顺利通过此圆弧形拱桥,并说明理由;
【答案】(1)![]() ;(2)能通过,理由见解析.
;(2)能通过,理由见解析.
【解析】
(1)如图,O是弧AB所在圆的圆心,连接OC,OB,设OB=OC=r,由垂径定理可得BD=6m,在Rt△BOD中,根据勾股定理列出方程求解即可;
(2)连接ON,根据题意求出OE,然后利用勾股定理求出EN即可得出结论.
解:(1)如图,O是弧AB所在圆的圆心,连接OC,OB,
由题意可知,O、C、D三点共线且OC⊥AB,
∴D为AB中点,
∵AB=12m,
∴BD=6m.
又∵CD=4m,
设OB=OC=r,则OD=(r4)m.
在Rt△BOD中,根据勾股定理得:r2=(r4)2+62,
解得r=![]() m;
m;
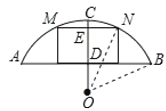
(2)此货船能顺利通过此圆弧形拱桥,
理由:如图,连接ON,
∵CD=4m,船舱顶部为长方形并高出水面3.4m,
∴CE=43.4=0.6(m),
∴OE=rCE=6.50.6=5.9(m),
在Rt△OEN中,EN2=ON2OE2=7.44,
∴EN=![]() ,
,
∴MN=2EN=5.4 m>5m,
∴此货船能顺利通过此圆弧形拱桥.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B=∠C=30°,点O是BC边上一点,以点O为圆心、OB为半径的圆经过点A,与BC交于点D.
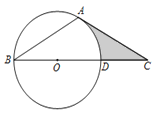
⑴ 试说明AC与⊙O相切;
⑵ 若![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)
(1)用含m,n的代数式表示所有裁剪线(图中虚线部分)的长度之和;
(2)观察图形,发现代数式2m2+5mn+2n2可以因式分解为 ;
(3)若每块小矩形的面积为10cm2,四个正方形的面积和为58cm2,试求(m+n)2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
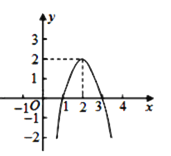
(1)写出方程ax2+bx+c=0的两个根;
(2)写出y随x的增大而减小的自变量x的取值范围;
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
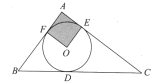
【题目】如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )
A.4B.6.25C.7.5D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方形ABCD和正方形BEFG如图(一)所示放置,已知AB=5![]() ,BE=6,将正方形BEFG绕点B顺时针旋转一定的角度α(0°≤α≤360°)到图(二)所示:连接AE,CG,
,BE=6,将正方形BEFG绕点B顺时针旋转一定的角度α(0°≤α≤360°)到图(二)所示:连接AE,CG,
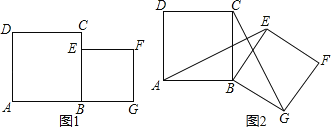
(1)求线段AE与CG的关系,并给出证明
(2)当旋转至某一个角度时,点C,E,G在同一条直线上,请画出示意图形,并求出此时AE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
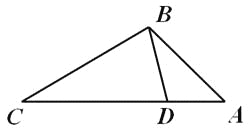
【题目】如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,不正确的是( )
A.∠ABD=∠CB.∠ADB=∠ABCC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
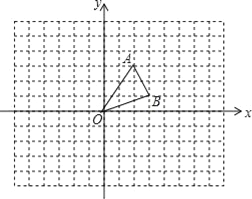
【题目】在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3)、B(3,1)、O(0,0).
(1)将△ABO向左平移4个单位,画出平移后的△A1B1O1.
(2)将△ABO绕点O顺时针旋转180°,画出旋转后得到的△A2B2O.此时四边形ABA2B2的形状是 .
(3)在平面上是否存在点D,使得以A、B、O、D为顶点的四边形是平行四边形,若存在请直接写出符合条件的所有点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com