
【题目】如图,△ABC中,∠B=∠C=30°,点O是BC边上一点,以点O为圆心、OB为半径的圆经过点A,与BC交于点D.
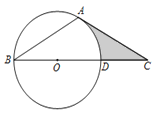
⑴ 试说明AC与⊙O相切;
⑵ 若![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OA,先得出∠OAB=30°,再解得∠OAC=90°,从而可判断出AC与⊙O的位置关系;
(2)连接AD,设OA的长度为x,根据“阴影部分的面积=△OAC的面积-扇形OAD的面积”列出方程即可求解.
⑴ 连接OA.
∵ OA=OB
∴ ∠OAB=∠B
∵ ∠B=30°
∴ ∠OAB=30°
△ABC中:∠B=∠C=30°
∴ ∠BAC=180°-∠B-∠C=120°
∴ ∠OAC=∠BAC-∠OAB=120°-30°=90°
∴ OA⊥AC
∴ AC是⊙O的切线,即AC与⊙O相切.
⑵ 连接AD.
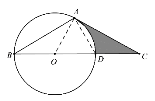
∵ ∠C=30°,∠OAC=90°
∴ OC=2OA
设OA的长度为x,则OC=2x
在△OAC中,∠OAC=90°,![]()
根据勾股定理可得:![]()
解得:![]() ,
,![]() (不合题意,舍去)
(不合题意,舍去)
∴![]() ,
,![]()
∴![]()
答:图中阴影部分的面积为![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点 A 在函数y1=-![]() (x>0)的图象上,点 B 在直线 y2=kx+1+k(k 为常数,且 k≥0)上.若 A,B 两点关于原点对称,则称点 A,B 为函数 y1,y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
(x>0)的图象上,点 B 在直线 y2=kx+1+k(k 为常数,且 k≥0)上.若 A,B 两点关于原点对称,则称点 A,B 为函数 y1,y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对B.只有1对
C.只有2对D.有2对或3对
查看答案和解析>>
科目:初中数学 来源: 题型:
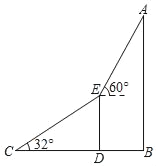
【题目】为庆祝改革开放40周年,深圳举办了灯光秀,某数学兴趣小组为测量“平安金融中心”AB的高度,他们在地面C处测得另一幢大厦DE的顶部E处的仰角∠ECD=32°.登上大厦DE的顶部E处后,测得“平安中心”AB的顶部A处的仰角为60°,(如图).已知C、D、B三点在同一水平直线上,且CD=400米,DB=200米.
(1)求大厦DE的高度;
(2)求平安金融中心AB的高度.
(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2)请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标.
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出A2的坐标.
(3)画出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
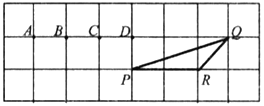
【题目】如图,![]() 在边长为1个单位的方格纸中,它的顶点在小正方形顶点位置,其中点
在边长为1个单位的方格纸中,它的顶点在小正方形顶点位置,其中点![]() 、
、![]() 、
、![]() 、
、![]() 也是小正方形的顶点,那么与
也是小正方形的顶点,那么与![]() 相似的是( )
相似的是( )
A.以点![]() 、
、![]() 、
、![]() 为顶点的三角形;
为顶点的三角形;
B.以点![]() 、
、![]() 、
、![]() 为顶点的三角形
为顶点的三角形
C.以点![]() 、
、![]() 、
、![]() 为顶点的三角形
为顶点的三角形
D.以点![]() 、
、![]() 、
、![]() 为顶点的三角形
为顶点的三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售某种冰箱,该种冰箱每台进价为2500元.已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了x元.
(1)填表(不需化简):
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
(2)商场为使这种冰箱平均每天的销售利润达到5000元,则每台冰箱的实际售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中: ①△BDE是等边三角形; ②AE∥BC; ③△ADE的周长是9; ④∠ADE=∠BDC.其中正确的序号是( )
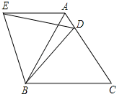
A.②③④B.①②④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
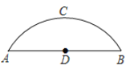
(1)求拱桥的半径;
(2)有一艘宽为5m的货船,船舱顶部为长方形,并高出水面3.4m,则此货船是否能顺利通过此圆弧形拱桥,并说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com