
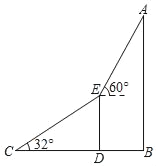
【题目】为庆祝改革开放40周年,深圳举办了灯光秀,某数学兴趣小组为测量“平安金融中心”AB的高度,他们在地面C处测得另一幢大厦DE的顶部E处的仰角∠ECD=32°.登上大厦DE的顶部E处后,测得“平安中心”AB的顶部A处的仰角为60°,(如图).已知C、D、B三点在同一水平直线上,且CD=400米,DB=200米.
(1)求大厦DE的高度;
(2)求平安金融中心AB的高度.
(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
【答案】(1)248米(2)594米
【解析】
(1)在Rt△DCE中,根据正切函数的定义即可求出大厦DE的高度;
(2)作EF⊥AB于F.由题意,得EF=DB=200米,BF=DE,∠AEF=60°.在Rt△AFE中,根据正切函数的定义得出AF=EFtan∠AEF,由AB=BF+AF即可得到结论.
(1)∵在Rt△DCE中,∠CDE=90°,∠ECD=32°,CD=400,∴DE=CDtan∠ECD≈400×0.62=248(米).
答:大厦DE的高度约为248米.
(2)如图,作EF⊥AB于F.
由题意,得:EF=DB=200,BF=DE=248,∠AEF=60°.
在Rt△AFE中,∵∠AFE=90°,∴AF=EFtan∠AEF≈200×1.73=346,∴AB=BF+AF=248+346=594(米).
答:平安金融中心AB的高度约为594米.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
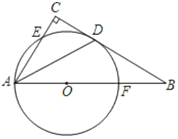
【题目】如图,在以线段AB为直径的⊙O上取一点,连接AC、BC.将△ABC沿AB翻折后得到△ABD.
(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC·AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线段AE、CB相交于点F,若BC=2,AC=4,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E,F分别为BC,CD上的点,且AE⊥BF,垂足为G.
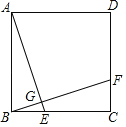
(1)求证:AE=BF;(2)若BE=![]() ,AG=2,求正方形的边长.
,AG=2,求正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 AB 为⊙O 的直径,BC⊥AB 于 B,且 BC=AB,D 为半圆⊙O 上的一点,连接 BD 并延长交半圆⊙O 的切线 AE 于 E.

(1)如图 1,若 CD=CB,求证:CD 是⊙O 的切线;
(2)如图 2,若 F 点在 OB 上,且CD⊥DF,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴发服装店老板用4500元购进一批某款T恤衫,由于深受顾客喜爱,很快售完,老板又用4950元购进第二批该款式T恤衫,所购数量与第一批相同,但每件进价比第一批多了9元.
(1)第一批该款式T恤衫每件进价是多少元?
(2)老板以每件120元的价格销售该款式T恤衫,当第二批T恤衫售出![]() 时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)
时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B=∠C=30°,点O是BC边上一点,以点O为圆心、OB为半径的圆经过点A,与BC交于点D.
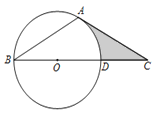
⑴ 试说明AC与⊙O相切;
⑵ 若![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D, 点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E、F.
(1)试判断直线BC与OD的位置关系,并说明理由.
(2)若BD=![]() ,BF=3,求⊙O的半径.
,BF=3,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
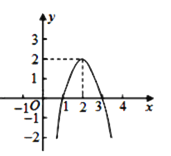
(1)写出方程ax2+bx+c=0的两个根;
(2)写出y随x的增大而减小的自变量x的取值范围;
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com