
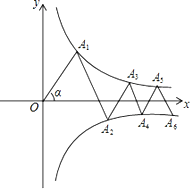
【题目】如图,点A1、A3、A5…在反比例函数![]() (x>0)的图象上,点A2、A4、A6……在反比例函数
(x>0)的图象上,点A2、A4、A6……在反比例函数![]() (x>0)的图象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,则An(n为正整数)的纵坐标为____________.(用含n的式子表示)
(x>0)的图象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,则An(n为正整数)的纵坐标为____________.(用含n的式子表示)
【答案】(-1)n+1![]()
【解析】
先证明△OA1E是等边三角形,求出A1的坐标,作高线A1D1,再证明△A2EF是等边三角形,作高线A2D2,设A2(x,![]() ),根据OD2=2+
),根据OD2=2+![]() =x,解方程可得到等边三角形的边长和A2的纵坐标,同理依次得出结论,并总结规律:发现点A1、A3、
=x,解方程可得到等边三角形的边长和A2的纵坐标,同理依次得出结论,并总结规律:发现点A1、A3、![]() 在
在![]() 轴上方,纵坐标为正,其它在下方,纵坐标为负,可以利用
轴上方,纵坐标为正,其它在下方,纵坐标为负,可以利用![]() 解决.
解决.
解:如图,过A1作A1D1⊥x轴于D1,
∵OA1=2,∠OA1A2=∠α=60°,
∴△OA1E是等边三角形,
OD1![]() =1,A1D1
=1,A1D1![]() =
=![]() ,
,
∴A1(1,![]() ),
),
∴k=![]() ,
,
∴两个反比例函数的式分别为:y=![]() 和y=
和y=![]() ,
,
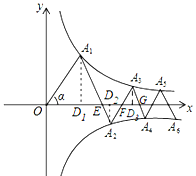
过A2作A2D2⊥x轴于D2,
∵∠A2EF=∠A1A2A3=60°,
∴△A2EF是等边三角形,
设A2(x,![]() ),则A2D2=
),则A2D2=![]() ,
,
Rt△EA2D2中,∠EA2D2=30°,
∴ED2=![]() ,
,
∵OD2=2+![]() =x,
=x,
解得:x1=1-![]() (舍),x2=1+
(舍),x2=1+![]() ,
,
∴EF=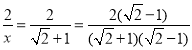 =2(
=2(![]() -1)=2
-1)=2![]() -2,
-2,
A2D2=![]() ,即A2的纵坐标为
,即A2的纵坐标为![]() ;
;
过A3作A3D3⊥x轴于D3,同理得:△A3FG是等边三角形,
设A3(x,![]() ),则A3D3=
),则A3D3=![]() ,
,
Rt△FA3D3中,∠FA3D3=30°,
∴FD3=![]() ,
,
∵OD3=![]() ,
,
解得:x1=![]() (舍),x2=
(舍),x2=![]() ;
;
∴GF=![]() ,
,
A3D3=![]() ,即A3的纵坐标为
,即A3的纵坐标为![]() ;…
;…
∴An(n为正整数)的纵坐标为:![]()
![]() .
.
故答案为:![]()
![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=﹣x2+2x+3的图象交x轴于点A、B(点A在点B的左侧).若把点B向上平移m(m>0)个单位长度得点B1,若点B1向左平移n(n>0)个单位长度,将与该二次函数图象上的点B2重合;若点B1向左平移(n+2)个单位长度,将与该二次函数图象上的点B3重合.则n的值为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
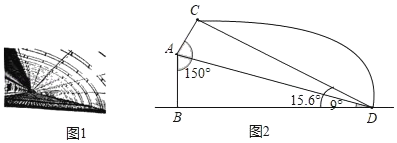
【题目】河南省政府为促进农业发展,加快农村建设,计划扶持兴建一批新型钢管装配式大棚,如图1所示线段AB、BD分别为大棚的墙高和跨度,AC表示保温板的长,已知墙高AB为3米,墙面与保温板所成的角∠BAC=150°,在点D处测得A点、C点的仰角分别为9°,15.6°,如图2所示求保温板AC的长是多少米?(精确到0.1米)(参考数据:sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 中,
中,![]() ,P是斜边AC上一个动点,以即为直径作
,P是斜边AC上一个动点,以即为直径作![]() 交BC于点D,与AC的另一个交点E,连接DE.
交BC于点D,与AC的另一个交点E,连接DE.
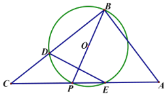
(1)当![]() 时,
时,
①若![]() ,求
,求![]() 的度数;
的度数;
②求证![]() ;
;
(2)当![]() ,
,![]() 时,
时,
①是含存在点P,使得![]() 是等腰三角形,若存在求出所有符合条件的CP的长;
是等腰三角形,若存在求出所有符合条件的CP的长;
②以D为端点过P作射线DH,作点O关于DE的对称点Q恰好落在![]() 内,则CP的取值范围为________.(直接写出结果)
内,则CP的取值范围为________.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=5,BC=6,点D、E分别是边AB、AC上的动点(点D、E不与△ABC的顶点重合),AD和BE交于点F,且∠AFE=∠ABC

(1)求证:△ABD∽△BCE;
(2)设AE=x,ADFD=y,求y关于x的函数关系式,并直接写出x的取值范围;
(3)当△AEF是等腰三角形时,求DF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
背景阅读:旋转就是将图形上的每一点在平面内绕着旋转中心旋转固定角度的位置移动,其中“旋”是过程,“转”是结果.旋转作为图形变换的一种,具备图形旋转前后对应点到旋转中心的距离相等:对应点与旋转中心所连线段的夹角等于旋转角:旋转前、后的图形是全等图形等性质.所以充分运用这些性质是在解决有关旋转问题的关健.
实践操作:如图1,在Rt△ABC中,∠B=90°,BC=2AB=12,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
问题解决:(1)①当α=0°时,![]() = ;②当α=180°时,
= ;②当α=180°时,![]() = .
= .
(2)试判断:当0°≤a<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
问题再探:(3)当△EDC旋转至A,D,E三点共线时,求得线段BD的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() ,且对称轴为直线
,且对称轴为直线![]() .
.
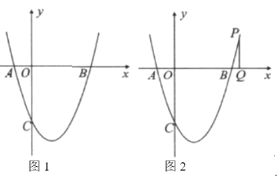
(1)求该抛物线的解析式;
(2)点![]() 是第四象限内抛物线上的一点,当
是第四象限内抛物线上的一点,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)如图2,点![]() 是抛物线上的一个动点,过点
是抛物线上的一个动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .当
.当![]() 时,直接写出点
时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 图象的一部分如图所示,顶点坐标为
图象的一部分如图所示,顶点坐标为![]() ,与
,与![]() 轴的一个交点的坐标为(-3,0),给出以下结论:①
轴的一个交点的坐标为(-3,0),给出以下结论:①![]() ;②
;②![]() ;③若
;③若![]() 、
、![]() 为函数图象上的两点,则
为函数图象上的两点,则![]() ;④当
;④当![]() 时方程
时方程![]() 有实数根,则
有实数根,则![]() 的取值范围是
的取值范围是![]() .其中正确的结论的个数为( )
.其中正确的结论的个数为( )
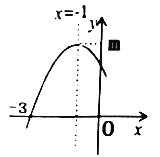
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com