
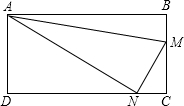
 如图,在矩形ABCD中,AB=24,BC=12,M、N两点分别从点B、C开始沿边BC和CD匀速运动,如果点M、N同时出发,它们运动的速度均为每秒2个单位长度,当点M到达终点C时,点N也停止运动,设运动的时间为t(s).下列说法:①当t=3时,MN∥BD;②当t=6时,△AMN的面积最小;③当t=4时,S△ABM=S△AND;④不存在MN与AN垂直的时刻,正确的有( )
如图,在矩形ABCD中,AB=24,BC=12,M、N两点分别从点B、C开始沿边BC和CD匀速运动,如果点M、N同时出发,它们运动的速度均为每秒2个单位长度,当点M到达终点C时,点N也停止运动,设运动的时间为t(s).下列说法:①当t=3时,MN∥BD;②当t=6时,△AMN的面积最小;③当t=4时,S△ABM=S△AND;④不存在MN与AN垂直的时刻,正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据题意分别求出CM、CN,根据平行线的判定定理判断①;根据题意列出函数关系式,根据二次函数的性质判断②;根据三角形的面积公式求出两个三角形的面积,比较判断③;根据勾股定理的逆定理计算,判断④.
解答 解:当t=3时,BM=6,CN=6,
∴CM=6,DN=18,
∴$\frac{CM}{CB}≠\frac{CN}{CD}$,
∴MN与BD不平行,①错误;
由题意得,△AMN的面积=四边形ABCD的面积-△ADN的面积-△NCM的面积-△ABM的面积
=288-$\frac{1}{2}$×12×(24-2t)$-\frac{1}{2}×$2t×(12-2t)-$\frac{1}{2}×$24×2t
=t2-12t+144
=(t-12)2,
当t≤12时,y随x的增大而减小,又0≤t≤6,
∴当t=6时,△AMN的面积最小,②正确;
当t=4时,S△ABM=$\frac{1}{2}×$24×8=96,
S△AND=$\frac{1}{2}$×12×(24-8)=96,
∴当t=4时,S△ABM=S△AND,③正确;
由题意得,AN2=AD2+DN2=144+(24-2t)2=4t2-96t+720,
MN2=CN2+CM2=8t2-48t+144,
AM2=AB2+BM2=4t2+576,
当MN与AN垂直时,4t2-96t+720+8t2-48t+144=4t2+576,
整理得,t2-18t+36=0,
解得,t1=9-3$\sqrt{5}$,t2=9+3$\sqrt{5}$(不合题意),
当t=9-3$\sqrt{5}$时,MN与AN垂直,④不正确;
故选:B.
点评 本题考查的是矩形的性质、平行线的判定、勾股定理的逆定理的应用,掌握平行线的判定定理、二次函数解析式的求法和二次函数的性质以及勾股定理的逆定理的应用是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 四边相等的四边形是正方形 | |
| B. | 四角相等的四边形是正方形 | |
| C. | 对角线互相垂直的平行四边形是正方形 | |
| D. | 有一个角是直角的菱形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
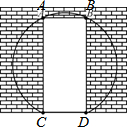 如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=$\frac{2}{3}\sqrt{3}$米.
如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=$\frac{2}{3}\sqrt{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 扩大原来的4倍 | C. | 扩大原来的8倍 | D. | 扩大原来的16倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查某品牌牛奶质量合格率 | |
| B. | 调查某幼儿园一班学生的平均身高 | |
| C. | 调查某市中小学生收看纪念抗日战争胜利70周年大阅兵的情况 | |
| D. | 调查某省九年级学生一周内网络自主学习的情况 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com