
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式从左到右依次计算即可得到结果;
(3)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解答 解:(1)原式=1$\frac{4}{7}$+$\frac{3}{7}$-$\frac{2}{3}$=2-$\frac{2}{3}$=1$\frac{1}{3}$;
(2)原式=-$\frac{6}{5}$×$\frac{5}{3}$×$\frac{3}{7}$=-$\frac{6}{7}$;
(3)原式=-8+$\frac{1}{5}$-$\frac{1}{5}$=-8.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
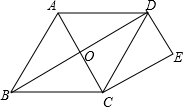 如图,O是菱形ABCD的对角线的交点,BC=2OC=2,DE=1,DE∥AC,
如图,O是菱形ABCD的对角线的交点,BC=2OC=2,DE=1,DE∥AC,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
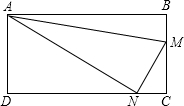 如图,在矩形ABCD中,AB=24,BC=12,M、N两点分别从点B、C开始沿边BC和CD匀速运动,如果点M、N同时出发,它们运动的速度均为每秒2个单位长度,当点M到达终点C时,点N也停止运动,设运动的时间为t(s).下列说法:①当t=3时,MN∥BD;②当t=6时,△AMN的面积最小;③当t=4时,S△ABM=S△AND;④不存在MN与AN垂直的时刻,正确的有( )
如图,在矩形ABCD中,AB=24,BC=12,M、N两点分别从点B、C开始沿边BC和CD匀速运动,如果点M、N同时出发,它们运动的速度均为每秒2个单位长度,当点M到达终点C时,点N也停止运动,设运动的时间为t(s).下列说法:①当t=3时,MN∥BD;②当t=6时,△AMN的面积最小;③当t=4时,S△ABM=S△AND;④不存在MN与AN垂直的时刻,正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
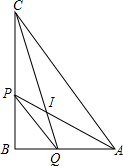 如图,在Rt△ABC中,∠B=90°,AP、CQ分别平分∠BAC、∠BCA,AP交CQ于I,连PQ,则S△IAC:S四边形ACPQ=1:2.
如图,在Rt△ABC中,∠B=90°,AP、CQ分别平分∠BAC、∠BCA,AP交CQ于I,连PQ,则S△IAC:S四边形ACPQ=1:2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com