
【题目】平面直角坐标系中,![]() 是坐标原点,抛物线
是坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 两点(如图),顶点是
两点(如图),顶点是![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]()
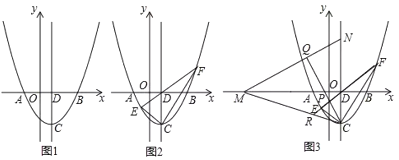
(1)如图(1)求抛物线的解析式;
(2)如图(2)![]() 是第三象限抛物线上一点,连接
是第三象限抛物线上一点,连接![]() 并延长交抛物线于点
并延长交抛物线于点![]() ,连接
,连接![]() 求证:
求证:![]() ;
;
(3)如图(3)在(2)问条件下,![]() 分别是线段
分别是线段![]() 延长线上一点,连接
延长线上一点,连接![]() ,过点
,过点![]() 作
作![]() 于
于![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,若
,若![]()
![]()
![]() 求点
求点![]() 坐标.
坐标.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)设DA=DB=m,根据抛物线对称性和OB=2OA,建立方程求解即可;
(2)配方法可求得抛物线顶点坐标,过点E作EH⊥CD于G,过F作FG⊥CD于G,可证明△DEH∽△DFG,tan∠GFC=tan∠ECH,即可证明∠ECF=90°;
(3)以DM为边在x轴上方作正方形DMKT,延长CQ交KT于S,过S作SG⊥DM于G,连接MT,作∠SCT平分线交MT于I,过点I作IJ⊥CT于J,设DM=t,则DT=TK=t,易证:△MDC≌△CJI,△MDN≌△SGP,可得:SZ=SL=t-7,CZ=CJ=t,CS=2t-7,利用勾股定理建立方程即可求得点M坐标,再利用相似三角形性质可求得点R坐标,运用待定系数法即可求得直线DR解析式,解方程组可求得点F的坐标.
解:(1)∵抛物线对称轴为:直线x=1,

∴D(1,0),由抛物线对称性知:DA=DB,设DA=DB=m,
则:A(1-m,0),B(1+m,0),
∵OB=2OA
∴1+m=2(m-1),解得:m=3
∴A(-2,0),B(4,0),将A(-2,0)代入![]() ,
,
得![]() ,
,
解得:![]() ;
;
∴抛物线的解析式为:![]() ;
;
(2)如图2,过点E作EH⊥CD于H,过F作FG⊥CD于G,
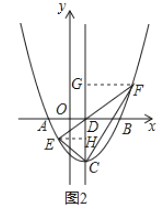
∵![]() ,
,
∴点C的坐标为:(1,![]() ),
),
设点E(n,![]() ),点F(m,
),点F(m,![]() ),
),
∴点G为:(1,![]() ),点H为:(1,
),点H为:(1,![]() ),
),
∴EH=1-n,FG=m-1,DG=![]() ,DH=
,DH=![]() ,
,
∵EH⊥CD,FG⊥CD
∴∠DHE=∠DGF=90°
∵∠EDH=∠FDG
∴△DEH∽△DFG,
∴![]() ,
,
得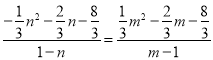 ,
,
得![]()
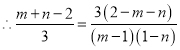
![]()
![]()


![]()
∴![]() ;
;
(3)如图3,以DM为边在x轴上方作正方形DMKT,延长CQ交KT于S,过S作SG⊥DM于G,连接MT,作∠SCT平分线交MT于I,过点I作IJ⊥CT于J,作IL⊥KT于L,作IZ⊥SQ于Z,设DM=t,则DT=TK=t,

∵正方形DMKT,
∴∠DTM=∠KTM=∠DMT=45°
∴四边形TLIJ是正方形,
∴IJ=TJ=TL
∵CI平分∠SCT
∴∠JCI=![]() ∠SCT
∠SCT
∵CQ⊥MN
∴∠SCT+∠MND=∠NMD+∠MND=90°
∴∠NMD=∠SCT
∵∠NMD=2∠DMC,
∴∠DMC=![]() ∠SCT
∠SCT
∴∠JCI=∠DMC
∴∠JCI+∠DTM=∠DMC+∠DMT
即∠CIM=∠CMI
∴CM=CI
∵∠MDC=∠CJI=90°
∴△MDC≌△CJI(AAS)
∴IJ=CD=3
∴JT=TL=3
在△MDN和△SGP中
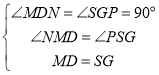
∴△MDN≌△SGP(AAS)
∴DN=PG
∵DN+BO=MP,MG+PG=MP
∴MG=BO=4
∴KS=4
∴SL=t-7,
易证:SZ=SL=t-7,CZ=CJ=t,CS=2t-7
在Rt△CST中,∵ST2+CT2=CS2
∴(t-4)2+(t+3)2=(2t-7)2,
解得:t1=12,t2=1(不符合题意,舍去)
∴M(-11,0);
过点R作RW⊥DM于W,则△MRW∽△MCD
∵MR:RC=7:3,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴点R为:(![]() ,
,![]() ),
),
设DR直线为![]() ,
,
则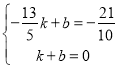 ,解得:
,解得: ,
,
![]() 解析式:
解析式:![]() ;
;
∴解方程组 ,
,
解得: ,
, ;
;
∴点E为:(![]() ,
,![]() ),点
),点![]() ;
;


科目:初中数学 来源: 题型:
【题目】某汽车销售公司一位销售经理1—5月份的汽车销售统计图如下:
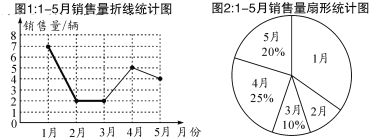
(1)已知1月的销售量是2月的销售量的3.5倍,则1月的销售量为________辆,在扇形图中,2月的销售量所对应的扇形的圆心角大小为________;
(2)补全图中销售量折线统计图;
(3)已知4月份销售的车中有3辆国产车和2辆合资车,国产车分别用G1,G2,G3表示,合资车分别用H1,H2表示,现从这5辆车中随机抽取两辆车参加公司的回馈活动,请用列举法(画树状图或列表)求出“抽到的两辆车都是国产车”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60 m到达点C,测得点B在点C的北偏东60°方向,如图②.
(1)求∠CBA的度数;
(2)求出这段河的宽(结果精确到1 m,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).

① ②
查看答案和解析>>
科目:初中数学 来源: 题型:
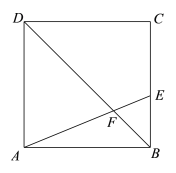
【题目】如图,在正方形ABCD中,E是BC边上的一点,连接AE交对角线BD于点F,将线段AE绕点A逆时针旋转90°,得到线段AG,连接EG,交对角线BD于点H,连接AH.
(1)根据题意补全图形;
(2)判断AH与EG的位置关系,并证明;
(3)若AB=2,设BE=x,BH=y,直接写出y关于x的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1的函数解析式为y=ax2-2x-3a,若抛物线C1经过点(0,-3).
(1)求抛物线C1的顶点坐标.
(2)已知实数x>0,请证明x+![]() ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+![]() =2;
=2;
(3)若将抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线C2,设A(m,y1),B(n,y2)是C2上的两个不同点,且满足:∠AOB=90,m>0,n<0.请你用含m的表达式表示出△AOB的面积S,并求出S的最小值及S取最小值时一次函数OA的函数解析式.(参考公式:在平面直角坐标系中,若P(x1,y1),Q(x2,y2),则P,Q两点间的距离为![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
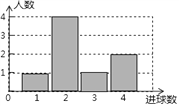
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 的图象如图所示;
的图象如图所示;
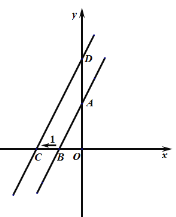
(1)直线与![]() 轴交点
轴交点![]() 的坐标是_____、与
的坐标是_____、与![]() 轴交点
轴交点![]() 的坐标______;
的坐标______;
(2)将直线![]() 沿
沿![]() 轴负半轴方向平移1个单位后得到直线
轴负半轴方向平移1个单位后得到直线![]() ,求直线与
,求直线与![]() 轴的交点
轴的交点![]() 的坐标;
的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com